
| a1=10 | a2=9.5 | a3= |
a4= |
… |
| b1=2 | b2= |
b3= |
b4= |
… |
| a1=10 | a2=9.5 | a3=9 | a4=8.5 | … |
| b1=2 | b2=3 | b3=4.5 | b4=6.75 | … |
|
|
| 20×1 |
| 2 |
| 1 |
| 2 |
2[1-(
| ||
1-
|


科目:高中数学 来源: 题型:
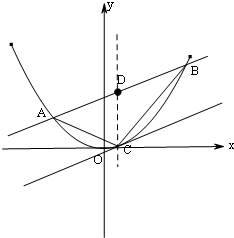 如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).查看答案和解析>>
科目:高中数学 来源: 题型:
 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,吴老师采用A、B两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图所示.记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,吴老师采用A、B两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图所示.记成绩不低于90分者为“成绩优秀”.| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+cn |
| 2 |
| an+bn |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=| π |
| 3 |
| CE |
| CC1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com