
| A. | $({0,{e^2}-\frac{1}{e}}]$ | B. | $({0,{e^2}+\frac{1}{e}}]$ | C. | $[{{e^2}-\frac{1}{e},+∞})$ | D. | $({-∞,{e^2}+\frac{1}{e}}]$ |
分析 令f(x)=0,求出a=-x2+2ex+$\frac{lnx}{x}$,构造函数h(x)=-x2+2ex+$\frac{lnx}{x}$,判断函数的单调性,根据函数单调性求出函数的最值.
解答 解:令f(x)=x2-2ex-$\frac{lnx}{x}$+a=0,
则a=-x2+2ex+$\frac{lnx}{x}({x>0})$,
设h(x)=-x2+2ex+$\frac{lnx}{x}$,
令h1(x)=-x2+2ex,h2(x)=$\frac{lnx}{x}$,
∴h2′(x)=$\frac{1-lnx}{x^2}$,发现函数h1(x),h2(x)在(0,e)上都是单调递增,在[e,+∞)上都是单调递减,
∴函数h(x)=-x2+2ex+$\frac{lnx}{x}$在(0,e)上单调递增,在[e,+∞)上单调递减,
故当x=e时,得h(x)min=e2+$\frac{1}{e}$,
∴函数f(x)至少存在一个零点需满足a≤h(x)max,
即a≤e2+$\frac{1}{e}$.
故选:D.
点评 本题考查了函数的图象与性质的应用问题,以及函数与方程的关系,进行解答,是易错题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:解答题
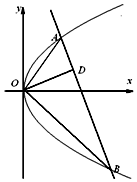 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
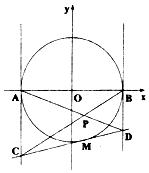 已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.
已知圆O:x2+y2=4与x轴交于A,B两点,点M为圆O上异于A,B的任意一点,圆O在点M处的切线与圆O在点A,B处的切线分别交于C,D,直线AD和BC交于点P,设P点的轨迹为曲线E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 16 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)在区间$[\frac{3π}{4},π]$上单调递增 | |
| C. | 函数f(x)的图象关于直线$x=-\frac{7π}{12}$对称 | |
| D. | 函数f(x)的图象关于点$(\frac{7π}{12},0)$对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com