
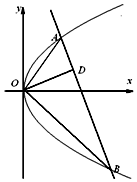
 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).分析 (Ⅰ)设点A的坐标(x1,y1),点B的坐标(x2,y2),点D的坐标为(x0,y0)(x0≠0),由OA⊥OB,得x1x2+y1y2=0,由此入手能求出点D的方程.
(Ⅱ)点D(2,1)代入方程x2+y2-2px=0,能求出结果.
解答 (本小题满分12分)
解:(Ⅰ)设点A的坐标(x1,y1),点B的坐标(x2,y2),点D的坐标为(x0,y0)(x0≠0),
由OA⊥OB得x1x2+y1y2=0.…(2分)
由已知,得直线AB的方程为${y_0}y=-{x_0}x+x_0^2+y_0^2$.…(3分)
又有$y_1^2=2p{x_1},y_2^2=2p{x_2},y_1^2y_2^2=(2p{x_1})(2p{x_2}),{x_1}{x_2}=\frac{y_1^2y_2^2}{{4{p^2}}}$,
由x1x2+y1y2=0得${y_1}{y_2}+4{p^2}=0$.…(4分)
把${y_0}y=-{x_0}x+x_0^2+y_0^2$代入y2=2px并消去x得${x_0}{y^2}+2p{y_0}y-2p(x_0^2+y_0^2)=0$,
得${y_1}{y_2}=\frac{-2p(x_0^2+y_0^2)}{x_0}$,…(6分)
代入${y_1}{y_2}+4{p^2}=0$
得$x_0^2+y_0^2-2p{x_0}=0({x_0}≠0)$,…(8分)
故所求点D的轨迹方程为x2+y2-2px=0(x≠0).…(10分)
(Ⅱ)把x=2,y=1代入方程x2+y2-2px=0中,得$p=\frac{5}{4}$.…(12分)
点评 本题考查点的轨迹方程的求法,考查实数值的求法,是中档题,解题时要认真审题,注意直线、抛物线的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (2,+∞) | C. | (1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{9}{4}$ | C. | 2 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,{e^2}-\frac{1}{e}}]$ | B. | $({0,{e^2}+\frac{1}{e}}]$ | C. | $[{{e^2}-\frac{1}{e},+∞})$ | D. | $({-∞,{e^2}+\frac{1}{e}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com