
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在平行四边形ABCD中,M、N分别为AB、AD上的点,且$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC、MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{11}$ | D. | $\frac{4}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -7 | C. | 12 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
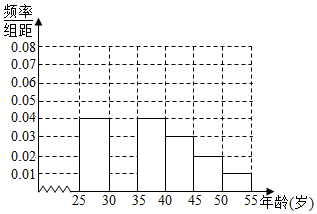
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
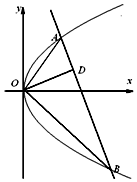 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com