
| A. | (-2,+∞) | B. | (2,+∞) | C. | (1,+∞) | D. | (0,+∞) |
分析 令g(x)=$\frac{f(x)}{{e}^{x}}$,利用导数和已知即可得出其单调性.再利用函数的奇偶性和已知可得g(0)=1,即可得出.
解答 解:令g(x)=$\frac{f(x)}{{e}^{x}}$,
则g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f′(x)<f(x),∴g′(x)<0.
∴g(x)在R上单调递减.
∵f(-x)=f(2+x),
∴f(x+1)=f(-x+1),
∴函数关于x=1对称,
∴f(0)=f(2)=1,
原不等式等价为g(x)<1,
∵g(0)=$\frac{f(0)}{{e}^{0}}$=1.
∴g(x)<1?g(x)<g(0),
∵g(x)在R上单调递减,
∴x>0.
∴不等式f(x)<ex的解集为(0,+∞),
故选:D.
点评 本题考查了利用导数研究函数的单调性、利用函数的单调性解不等式、函数的奇偶性及对称性,属于难题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -7 | C. | 12 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
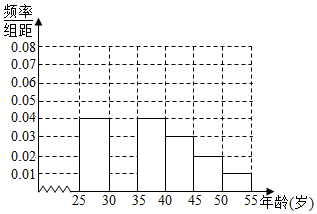
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | q |
| 第六组 | [50,55) | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
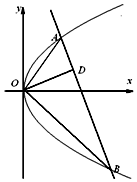 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元)
某人上午7时乘船出发,以匀速v海里/小时(4≤v≤20)从A港前往相距50海里的B地,然后乘汽车以匀速ω千米/小时(30≤ω≤100)自B港前往相距300千米的C市,计划当天下午4到9时到达C市.设乘船和汽车的所要的时间分别为x、y小时,如果所需要的经费P=100+3(5-x)+(8-y)(单位:元) 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 16 | C. | 12 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com