
已知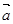 =(
=(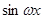 ,
,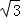
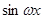 ),
), =(
=(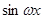 ,
,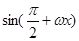 ),(ω>0),
),(ω>0),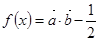 且
且 的最小正周期是
的最小正周期是 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若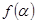 =
=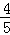 (
(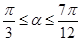 ),求
),求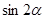 值;
值;
(Ⅲ)若函数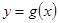 与
与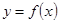 的图象关于直线
的图象关于直线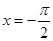 对称,且方程
对称,且方程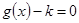 在区间
在区间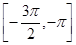 上有解,求
上有解,求 的取值范围.
的取值范围.
(1) ;(2)
;(2)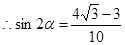 ;(3)
;(3)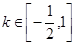 .
.
解析试题分析:1)先用数量积的概念转化为三角函数的形式,寻求角与角之间的关系,化非特殊角为特殊角;正确灵活运用公式,通过三角变换消去或约去一些非特殊角的三角函数值,注意题中角的范围;(2)掌握一些常规技巧:“1”的代换,和积互化等,异名三角函数化为同名三角函数,异角化为同角,异次化为同次,切化弦,特殊角与特殊角的三角函数互化;(3)注意利用转化的思想,本题转化为求最值,熟悉公式的整体结构,体会公式间的联系,倍角公式和辅助角公式应用是重点.
试题解析:解:(1)由题意可得
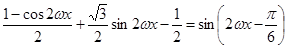 且
且 的周期为
的周期为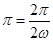 ,求得
,求得 .
.
Ⅱ)由(Ⅰ)得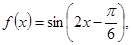 根据
根据
 ,
,
可得 ,
,

(Ⅲ)由于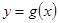 与
与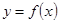 的图像关于直线
的图像关于直线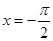 对称,
对称,
区间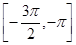 关于直线
关于直线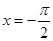 的对称区间
的对称区间 ,
,
故本题即求函数
 上的取值范围,
上的取值范围,
令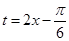 ,
,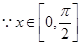 ,可得
,可得 ,
,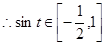 ,
,
即 的范围为
的范围为
考点:(1)三角函数的变换;(2)三角函数求值域.


科目:高中数学 来源: 题型:解答题
已知向量a=(cosθ,sinθ),θ∈[0,π],向量b=(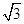 ,-1).
,-1).
(1)若a⊥b,求θ的值;
(2)若|2a-b|<m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)本题共有2个小题,第1小题满分4分,第2个小题满分8分。
已知复数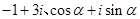 (
(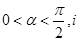 是虚数单位)在复平面上对应的点依次为
是虚数单位)在复平面上对应的点依次为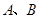 ,点
,点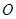 是坐标原点.
是坐标原点.
(1)若 ,求
,求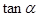 的值;
的值;
(2)若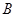 点的横坐标为
点的横坐标为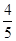 ,求
,求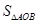 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
平面内动点P到点F(1,0)的距离等于它到直线x=-1的距离,记点P的轨迹为曲线Γ.
(1)求曲线Γ的方程;
(2)若点A,B,C是Γ上的不同三点,且满足 +
+ +
+ =0,证明:△ABC不可能为直角三角形.
=0,证明:△ABC不可能为直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com