
分析 对n分类讨论,利用等差数列的前n项和公式即可得出.
解答 解:设Sn=12-22+32-42+…+(-1)n+1n2.
当n=2k(k∈N*)时,Sn=(12-22)+(32-42)+…+[(n-1)2-n2]
=(1-2)(1+2)+(3-4)(3+4)+…+(n-1-n)(n-1+n)
=-(1+2+3+…+n)=-$\frac{n(n+1)}{2}$.
当n=2k-1(k∈N*)时,Sn=Sn-1+n2=n2-$\frac{n(n-1)}{2}$=$\frac{n(n+1)}{2}$.
∴Sn=$\left\{\begin{array}{l}{-\frac{n(n+1)}{2},n为偶数}\\{\frac{n(n+1)}{2},n为奇数}\end{array}\right.$.
点评 本题考查了等差数列的通项公式及其前n项和公式、分组求和,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{15}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 5 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{4}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{3}{4}$ | D. | -log37 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
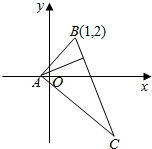 如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求:
如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com