
【题目】在平面直角坐标系![]() 中,已知中心在坐标原点,焦点在坐标轴上的椭圆
中,已知中心在坐标原点,焦点在坐标轴上的椭圆![]() 的右焦点为
的右焦点为![]() ,且离心率
,且离心率![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,过
的中点,过![]() 作直线
作直线![]() 的垂线
的垂线![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
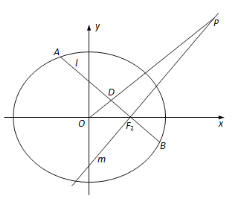
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)证明:点![]() 在一条定直线上;
在一条定直线上;
(3)当![]() 最大时,求
最大时,求![]() 的面积.
的面积.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)由焦点坐标、离心率和椭圆![]() 关系可构造方程组求得
关系可构造方程组求得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设![]() ,与椭圆方程联立得到韦达定理的形式,进而得到
,与椭圆方程联立得到韦达定理的形式,进而得到![]() 中点
中点![]() 的坐标,进而得到直线
的坐标,进而得到直线![]() 方程,与直线
方程,与直线![]() 方程联立后可求得
方程联立后可求得![]() 点坐标,知
点坐标,知![]() 点横坐标为定值
点横坐标为定值![]() ,从而得到结论;
,从而得到结论;
(3)利用直线![]() 和
和![]() 的斜率可结合两角和差正切公式表示出
的斜率可结合两角和差正切公式表示出![]() ,利用基本不等式可求得
,利用基本不等式可求得![]() 的最大值,由取等条件可得此时
的最大值,由取等条件可得此时![]() 的值和
的值和![]() 点坐标;利用弦长公式和点到直线距离公式分别求得三角形的底和高,进而得到所求面积.
点坐标;利用弦长公式和点到直线距离公式分别求得三角形的底和高,进而得到所求面积.
(1)![]() 椭圆
椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为:
的标准方程为:![]() .
.
(2)设![]() ,
,![]() ,
,![]() 中点
中点![]() ,直线
,直线![]() :
:![]() ,
,
联立方程组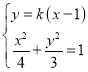 ,化简得:
,化简得:![]() ,
,
![]() ,
,![]() ,
,
将![]() 代入直线
代入直线![]() 的方程,得点
的方程,得点![]() 的坐标为
的坐标为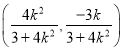 ,
,
![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() .
.
![]() 直线
直线![]() 过椭圆的右焦点
过椭圆的右焦点![]() 且与直线
且与直线![]() 垂直,
垂直,![]() 直线
直线![]() 的方程为
的方程为![]() .
.
解方程组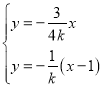 得:
得: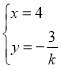 ,
,
![]() 点
点![]() 在定直线
在定直线![]() 上.
上.
(3)设直线![]() 的倾斜角为
的倾斜角为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() .
.
由(2)可知:![]() ,
,![]() .
.
![]()
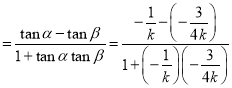
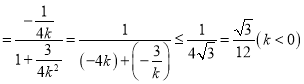 .
.
当且仅当![]() ,即
,即![]() 时
时![]() 取最大值,此时
取最大值,此时![]() 最大.
最大.
此时直线![]() 方程为
方程为![]() ,点
,点![]() 为
为![]() .
.
由(2)可得:![]() ,
,![]() ,
,![]() ,
,
![]() 弦长
弦长![]() ,
,![]() 到直线
到直线![]() 的距离
的距离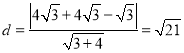 ,
,
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第![]() 条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第
条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第![]() 条规定:对不礼让行人的驾驶员处以扣
条规定:对不礼让行人的驾驶员处以扣![]() 分,罚款
分,罚款![]() 元的处罚.下表是某市一主干路口监控设备所抓拍的
元的处罚.下表是某市一主干路口监控设备所抓拍的![]() 个月内驾驶员不“礼让斑马线”行为统计数据:
个月内驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
不“礼让斑马线”驾驶员人数 |
|
|
|
|
|
(1)请利用所给数据求不“礼让斑马线”驾驶员人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ,并预测该路口
,并预测该路口![]() 月份的不“礼让斑马线”驾驶员人数;
月份的不“礼让斑马线”驾驶员人数;
(2)若从表中![]() 月份和
月份和![]() 月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为
月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为![]() 的样本,再从这
的样本,再从这![]() 人中任选
人中任选![]() 人进行交规调查,求抽到的两人恰好来自同一月份的概率.
人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式: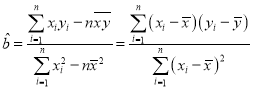 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,点E是
,点E是![]() 的中点,点F在边
的中点,点F在边![]() 上移动.
上移动.
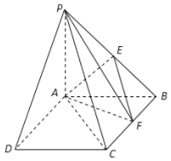
(Ⅰ)若F为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)若二面角![]() 的余弦值等于
的余弦值等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,
,![]() ,
,![]() 是其左右顶点,点
是其左右顶点,点![]() 是椭圆
是椭圆![]() 上任一点,且
上任一点,且![]() 的周长为6,若
的周长为6,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆![]() 于
于![]() ,
,![]() 两个不同点,证明:直线
两个不同点,证明:直线![]() 与
与![]() 的交点在一条定直线上.
的交点在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司新开发一电子产品,该电子产品的一个系统G有3个电子元件组成,各个电子元件能否正常工作的概率均为![]() ,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
(1)求系统不需要维修的概率;
(2)该电子产品共由3个系统G组成,设E为电子产品需要维修的系统所需的费用,求![]() 的分布列与期望;
的分布列与期望;
(3)为提高G系统正常工作概率,在系统内增加两个功能完全一样的其他品牌的电子元件,每个新元件正常工作的概率均为![]() ,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:
,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:![]() 满足什么条件时,可以提高整个G系统的正常工作概率?
满足什么条件时,可以提高整个G系统的正常工作概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意
,且对任意![]() ,
,![]() (s,k,l,
(s,k,l,![]() )都有
)都有![]() ,则称数列
,则称数列![]() 为“T”数列.
为“T”数列.
(1)证明:正项无穷等差数列![]() 是“T”数列;
是“T”数列;
(2)记正项等比数列![]() 的前n项之和为
的前n项之和为![]() ,若数列
,若数列![]() 是“T”数列,求数列
是“T”数列,求数列![]() 公比的取值范围;
公比的取值范围;
(3)若数列![]() 是“T”数列,且数列
是“T”数列,且数列![]() 的前n项之和
的前n项之和![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com