
分析 (Ⅰ)根据抛物线C经过点P(1,2),求抛物线C的方程;
(Ⅱ)由题意,直线PA与PB的倾斜角互补,所以kPA+kPB=0,求出A,B的坐标,即可得出结论.
解答 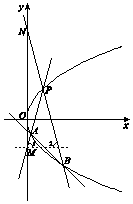 解:(Ⅰ)依题意,设抛物线C的方程为y2=ax(a≠0).[(1分)]
解:(Ⅰ)依题意,设抛物线C的方程为y2=ax(a≠0).[(1分)]
由抛物线C经过点P(1,2),
得a=4,[(3分)]
所以抛物线C的方程为y2=4x.[(4分)]
(Ⅱ)因为|PM|=|PN|,
所以∠PMN=∠PNM,
所以∠1=∠2,
所以直线PA与PB的倾斜角互补,
所以kPA+kPB=0.[(6分)]
依题意,直线AP的斜率存在,设直线AP的方程为:y-2=k(x-1)(k≠0),
将其代入抛物线C的方程,整理得k2x2-2(k2-2k+2)x+k2-4k+4=0.[(8分)]
设A(x1,y1),则x1=$\frac{{k}^{2}-4k+4}{{k}^{2}}$,y1=$\frac{4}{k}$-2,[(10分)]
所以A($\frac{{k}^{2}-4k+4}{{k}^{2}}$,$\frac{4}{k}$-2).[(11分)]
以-k替换点A坐标中的k,得B($\frac{(k+2)^{2}}{{k}^{2}}$,-$\frac{4}{k}$-2.[(12分)]
所以 kAB=$\frac{\frac{4}{k}-(-\frac{4}{k})}{\frac{(k-2)^{2}}{{k}^{2}}-\frac{(k+2)^{2}}{{k}^{2}}}$=-1,
所以直线AB的斜率为-1.[(14分)]
点评 本题考查抛物线的方程,考查直线与抛物线位置关系的运用,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {-1,2} | C. | $\{0,\frac{1}{2}\}$ | D. | $\{\frac{1}{2},2\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x±2\sqrt{2}y=0$ | B. | $2\sqrt{2}x±y=0$ | C. | x±8y=0 | D. | 8x±y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 65 | C. | 80 | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com