已知函数f(x)=ax3+bx2+cx+d在(-∞,1)上单调递减,在(1,3)上单调递增在(3,+∞)上单调递减,且函数图象在(2,f(2))处的切线与直线5x+y=0垂直.
(Ⅰ)求实数a、b、c的值;
(Ⅱ)设函数f(x)=0有三个不相等的实数根,求d的取值范围.
【答案】
分析:(Ⅰ)对函数求导可得,f′(x)=3ax
2+2bx+c,由题意可得

,所以f′(1)=2a+2b+c=0,f′(3)=27a+6b+c=0.联立可求a,b,c
(Ⅱ)由(Ⅰ)可得f(x),由x=1和x=3分别是函数f(x)的极小值点和极大值点,且当x取负值且绝对值足够大时,y取正值,当x时正值且足够大时,y取负值,则方程f(x)=0有三个不相等的实数根的充要条件为
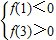
,代入可求
解答:解:(Ⅰ)对函数求导可得,f′(x)=3ax
2+2bx+c,
∵函数图象在(2,f(2))处的切线与直线5x+y=0垂直,
∴
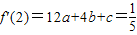
.①
由已知可知,1和3为方程f′(x)=0的两根,所以f′(1)=2a+2b+c=0,②
f′(3)=27a+6b+c=0.③
由①、②、③解得

,
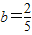
,
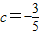
.(6分)
(Ⅱ)由(Ⅰ)得
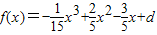
,
∵x=1和x=3分别是函数f(x)的极小值点和极大值点,且当x取负值且绝对值足够大时,y取正值,当x时正值且足够大时,y取负值.(8分)
所以方程f(x)=0有三个不相等的实数根的充要条件为

即
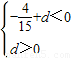
所以d的取值范围为

.(12分)
点评:本题主要考查了导数的几何意义:导数在某点处的导数即为改点的切线的斜率,导数的极值存在的条件的应用及利用函数与方程的相互转化求解参数的范围,属于导数知识的综合应用.

 ,所以f′(1)=2a+2b+c=0,f′(3)=27a+6b+c=0.联立可求a,b,c
,所以f′(1)=2a+2b+c=0,f′(3)=27a+6b+c=0.联立可求a,b,c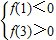 ,代入可求
,代入可求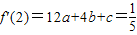 .①
.① ,
,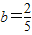 ,
,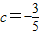 .(6分)
.(6分)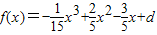 ,
, 即
即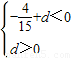
 .(12分)
.(12分)

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案