
| e1 |
| e2 |
| x |
| e1 |
| e2 |
| y |
| e1 |
| e2 |
| x |
| y |
| x |
| y |
| x |
| y |
| e1 |
| e2 |
| x |
| e1 |
| e2 |
| y |
| e1 |
| e2 |
| x |
| y |
| x |
| y |
| x |
| 5k2+2k+13 |
| y |
| 29 |
| x |
| y |
| x |
| y |
| ||||
|
|
| 2k-38 | ||||
2
|
| x |
| y |
| 2k-38 | ||||
2
|
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |


科目:高中数学 来源: 题型:
| A、x-4y+3=0 |
| B、x-4y-3=0 |
| C、4x+y-3=0 |
| D、4x-y-3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3600无后,逐步偿还转让费(不计息).在甲提供的资料中有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需要各种开支2000元.
在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3600无后,逐步偿还转让费(不计息).在甲提供的资料中有:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需要各种开支2000元.查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
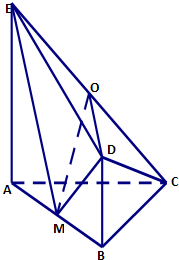 如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AB=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
如图,平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AB=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| b |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com