
分析 先根据约束条件画出可行域,设z1=$\frac{y}{x}$,再利用z1的几何意义求最值得出$\frac{y}{x}$的取值范围,最后将μ=$\frac{{x}^{2}+{y}^{2}}{xy}$表示为$\frac{y}{x}$的函数,即可解出μ=$\frac{{x}^{2}+{y}^{2}}{xy}$的取值范围.若ax+y$≥\frac{{y}^{2}}{x}$恒成立,则a≥t2-t,求出右边的最大值,即可求得实数a的取值范围
解答 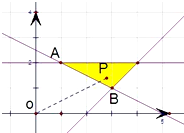 解:在平面直角坐标系上作出可行域后,
解:在平面直角坐标系上作出可行域后,
原点与可行域内任意一点的连线的斜率即$\frac{y}{x}$,
易求当连线过点A(1,2)时最大,最大值为2;当连线过点B(3,1)时最小,最小值为$\frac{1}{3}$
∴$\frac{y}{x}$∈[$\frac{1}{3}$,2],
设t=$\frac{y}{x}$∈[$\frac{1}{3}$,2],
μ=$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{y}{x}$+$\frac{x}{y}$=t+$\frac{1}{t}$∈[2,$\frac{10}{3}$];
若ax+y$≥\frac{{y}^{2}}{x}$恒成立,则a≥t2-t,
∵t∈[$\frac{1}{3}$,2],
∴t2-t=(t-$\frac{1}{2}$)2-$\frac{1}{4}$$∈[-\frac{1}{4},2]$,
∴a≥2.
故答案为:[2,$\frac{10}{3}$];a≥2.
点评 本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(5)>f(4) | B. | f(2)=f(4) | C. | f(0)<f(-1) | D. | f(2)<f($\sqrt{15}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com