
【题目】已知函数y=f(x)在R上的图象是连续不断的一条曲线,且图象关于原点对称,其导函数为f'(x),当x>0时,x2f'(x)>﹣2xf(x)成立,若x∈R,e2xf(ex)﹣a2x2f(ax)>0恒成立,则a的取值范围是_____.
【答案】0≤a<e
【解析】
构造g(x)=x2f(x),利用x2f'(x)>﹣2xf(x),可得g(x)在(0,+∞)上单调递增,转化e2xf(ex)﹣a2x2f(ax)>0,为g(ex)>g(ax),即可得ex>ax,分x=0,x>0,x<0三种情况讨论,参变分离即得解.
令g(x)=x2f(x),
因为x>0时,x2f'(x)>﹣2xf(x)
可知x>0时g'(x)=2xf(x)+x2f(x)>0,
g(x)在(0,+∞)上单调递增,
又因为函数y=f(x)在R上的图象是连续不断的一条曲线,且图象关于原点对称,
所以g(x)为R上单调递增的奇函数,
因为e2xf(ex)﹣a2x2f(ax)>0,所以g(ex)>g(ax),
即可得ex>ax,
当x=0时,1>0恒成立,
当x>0时,a![]() 恒成立,所以a
恒成立,所以a![]() ,
,
当x<0时,a![]() 恒成立,所以
恒成立,所以![]() ,
,
令h(x)![]() ,h'(x)
,h'(x)![]() ,
,
所以h(x)在(﹣∞,0),(0,1)上单调递减,在(1,+∞)上单调递增,
h(1)=e,
当x<0时,h(x)<0,
所以0≤a<e,


科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且(a+b﹣c)(sinA+sinB+sinC)=bsinA.
(1)求C;
(2)若a=2,c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记[x]为不超过实数x的最大整数,例如,[2]=2,[1.5]=1,[-0.3]=-1.设a为正整数,数列{xn}满足x1=a,xn+1=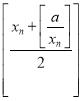 (n∈N*).现有下列命题:
(n∈N*).现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时,xn>![]() -1;
-1;
④对某个正整数k,若xk+1≥xk,则xk=[![]() ].
].
其中的真命题有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,ABCD为矩形,
中,ABCD为矩形,![]() 是以
是以![]() 为直角的等腰直角三角形,平面
为直角的等腰直角三角形,平面![]() 平面ABCD.
平面ABCD.

(1)证明:平面![]() 平面PBC;
平面PBC;
(2)![]() 为直线PC的中点,且
为直线PC的中点,且![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() >
>![]() >0
>0![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点![]() 作直线
作直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 都只有一个交点.求证:
都只有一个交点.求证:![]() ⊥
⊥![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,以
为极点,以![]() 轴正半轴建立极坐标系,曲线
轴正半轴建立极坐标系,曲线![]() 的极坐标系方程为
的极坐标系方程为![]() .
.
(1)写出直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com