已知a、b、c、d∈R+，且满足下列两个条件：
①a、b分别为回归直线方程y=bx+a的常数项和一次项系数，其中x与y之间有如下对应数据：
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
②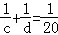
；则ac+bd的最小值是 ．
科目：高中数学 来源：[同步]2014年人教A版选修一1-2第一章1.2练习卷（解析版） 题型：选择题
（2009•韶关二模）以下五个命题
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②样本方差反映了样本数据与样本平均值的偏离程度；
③在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；
④在回归直线方程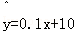
中，当解释变量x每增加一个单位时，预报变量
增加0.1个单位；
⑤在一个2×2列联表中，由计算得k2=13.079，则其两个变量间有关系的可能性是90%以上．
其中正确的是（ ）
A.②③④⑤ B.①③④ C.①③⑤ D.②④
查看答案和解析>>
科目：高中数学 来源：[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷（解析版） 题型：解答题
（12分）已知直线l：mx﹣2y+2m=0（m∈R）和椭圆C：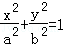
（a＞b＞0），椭圆C的离心率为
，连接椭圆的四个顶点形成四边形的面积为2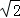
．
（1）求椭圆C的方程；
（2）设直线l经过的定点为Q，过点Q作斜率为k的直线l′与椭圆C有两个不同的交点，求实数k的取值范围；
（3）设直线l与y轴的交点为P，M为椭圆C上的动点，线段PM长度的最大值为f（m），求f（m）的表达式．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷（解析版） 题型：选择题
（5分）椭圆5x2+ky2=5的一个焦点是（0，﹣2），则k的值为（ ）
A.1 B.﹣1 C.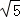
D.﹣
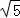
查看答案和解析>>
科目：高中数学 来源：[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型（解析版） 题型：填空题
设任意实数x0＞x1＞x2＞x3＞0，要使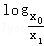
1993+
1993+
1993≥k•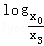
1993恒成立，则k的最大值是 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型（解析版） 题型：选择题
已知实数x，y分别满足：（x﹣3）3+2014（x﹣3）=1，（2y﹣3）3+2014（2y﹣3）=﹣1，则x2+4y2+4x的最小值是（ ）
A.0 B.26 C.28 D.30
查看答案和解析>>
科目：高中数学 来源：[同步]人教B版选修4-5 1.1不等式的性质和一元二次不等式的解法（解析版） 题型：选择题
（2014•上饶一模）已知函数f（x）的定义域为（﹣∞，+∞），f′（x）为f（x）的导函数，函数y=f′（x）的图象如图所示，且f（﹣2）=1，f（3）=1，则不等式f（x2﹣6）＞1的解集为（ ）
A.（2，3）
B.（﹣
，）
C.（2，3）∪（﹣3，﹣2）
D.（﹣∞，﹣）∪（，+∞）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=
=4.5，
=
=3.5．
=
，
=3.5﹣0.7×4.5=0.35=
．
=
=
=
=20
时取等号．
函数
．
的最小正周期。
的值。
，求
的值。
B．
C．
D．