
(12分)已知直线l:mx﹣2y+2m=0(m∈R)和椭圆C: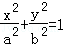 (a>b>0),椭圆C的离心率为
(a>b>0),椭圆C的离心率为 ,连接椭圆的四个顶点形成四边形的面积为2
,连接椭圆的四个顶点形成四边形的面积为2 .
.
(1)求椭圆C的方程;
(2)设直线l经过的定点为Q,过点Q作斜率为k的直线l′与椭圆C有两个不同的交点,求实数k的取值范围;
(3)设直线l与y轴的交点为P,M为椭圆C上的动点,线段PM长度的最大值为f(m),求f(m)的表达式.
(1)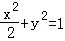 .(2)
.(2) .(3)f(m)=
.(3)f(m)=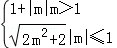 .
.
【解析】
试题分析:(1)直接利用离心率为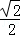 ,以及连接椭圆的四个顶点形成四边形的面积为2
,以及连接椭圆的四个顶点形成四边形的面积为2 列出关于a,b,c方程,求出a,b,c即可得到椭圆方程;
列出关于a,b,c方程,求出a,b,c即可得到椭圆方程;
(2)先求出直线所过的顶点坐标,再联立直线方程与椭圆方程,利用判别式大于0即可求实数k的取值范围;
(3)先求出点P的坐标(0,m),设出点M,根据两点间的距离公式求出|PM|2的表达式,根据M为椭圆C上的动点的限制对m分情况讨论即可求出f(m)的表达式.
【解析】
(1)由离心率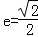 ,得
,得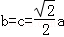
又因为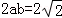 ,所以
,所以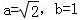 ,即椭圆标准方程为
,即椭圆标准方程为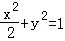 .(4分)
.(4分)
(2)由l:mx﹣2y+2m=0经过定点Q(﹣2,0),则直线l′:y=k(x+2),
由 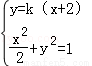 有(2k2+1)x2+8k2x+8k2﹣2=0.
有(2k2+1)x2+8k2x+8k2﹣2=0.
所以△=64k4﹣8(2k2+1)(4k2﹣1)>0,可化为 2k2﹣1<0
解得 . (8分)
. (8分)
(3) 由l:mx﹣2y+2m=0,设x=0,则y=m,所以P(0,m).
设M(x,y)满足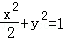 ,
,
则|PM|2=x2+(y﹣m)2=2﹣2y2+(y﹣m )2=﹣y2﹣2my+m2+2=﹣(y+m)2+2m2+2,
因为﹣1≤y≤1,所以
当|m|>1时,|MP|的最大值f(m)=1+|m|;
当|m|≤1时,|MP|的最大值f(m)=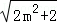 ;
;
所以f(m)=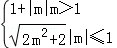 .(12分)
.(12分)


科目:高中数学 来源: 题型:
| a(x-1)(x-3) |
| A、-1 | B、-2 | C、-3 | D、-4 |
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.1练习卷(解析版) 题型:选择题
已知,如图,在梯形ABCD中,AD∥BC,AD=3,BC=7,点M,N分别是对角线BD,AC的中点,则MN=( )
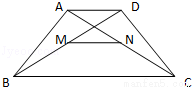
A.2 B.5 C.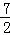 D.
D.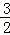
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2014•韶关二模)由于工业化城镇化的推进,大气污染日益加重,空气质量逐步恶化,雾霾天气频率增大,大气污染可引起心悸、胸闷等心脏病症状.为了解某市患心脏病是否与性别有关,在某医院心血管科随机的对入院50位进行调查得到了如表:
| 患心脏病 | 不患心脏病 | 合计 |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
参考临界值表:
p(p2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=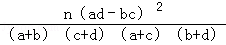 其中n =a +b +c +d).
其中n =a +b +c +d).
问有多大的把握认为是否患心脏病与性别有关.答:( )
A.95% B.99% C.99.5% D.99.9%
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•呼和浩特一模)已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )
A.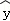 =1.23x+4 B.
=1.23x+4 B.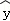 =1.23x﹣0.08 C.
=1.23x﹣0.08 C.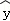 =1.23x+0.8 D.
=1.23x+0.8 D.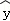 =1.23x+0.08
=1.23x+0.08
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•湖北)根据如下样本数据,得到回归方程 =bx+a,则( )
=bx+a,则( )
x | 3 | 4 | 5 | 6 | 7 | 8 |
y | 4.0 | 2.5 | ﹣0.5 | 0.5 | ﹣2.0 | ﹣3.0 |
A.a>0,b>0 | B.a>0,b<0 | C.a<0,b>0 | D.a<0,b<0 |
|
|
|
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)椭圆的中心在原点,焦距为4,一条准线为x=﹣4,则该椭圆的方程为( )
A.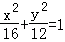 B.
B. C.
C.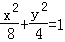 D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:填空题
已知a、b、c、d∈R+,且满足下列两个条件:
①a、b分别为回归直线方程y=bx+a的常数项和一次项系数,其中x与y之间有如下对应数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
②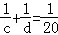 ;则ac+bd的最小值是 .
;则ac+bd的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com