
分析 (Ⅰ)运用分段函数的解析式,可得f($\frac{1}{2}$)=$\frac{7}{4}$,解方程可得p=1;
(Ⅱ)求出f(x)的解析式,画出图象,f(x)-m=0有3个不同的解,即为y=f(x)与y=m有3个交点,由图象观察,即可得到所求m的范围;
(Ⅲ)由(Ⅱ)知,当x∈[-1,16]时,f(x)∈[0,4].由题意可得n+1≥f(x)max=4,即可得到所求范围.
解答 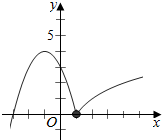 解:(Ⅰ)∵f[f($\sqrt{2}$)]=$\frac{7}{4}$,即f($\frac{1}{2}$)=$\frac{7}{4}$,
解:(Ⅰ)∵f[f($\sqrt{2}$)]=$\frac{7}{4}$,即f($\frac{1}{2}$)=$\frac{7}{4}$,
∴-($\frac{1}{2}$+1)2+4p=$\frac{7}{4}$,∴p=1;
(Ⅱ)由(Ⅰ)知,f(x)=$\left\{\begin{array}{l}{-(x+1)^{2}+4,x<1}\\{lo{g}_{2}x,x≥1}\end{array}\right.$,
其大致图象如右:
f(x)-m=0有3个不同的解,即为y=f(x)与y=m有3个交点,
∴实数m的取值范围为0<m<4;
(Ⅲ)由(Ⅱ)知,当x∈[-1,16]时,f(x)∈[0,4].
∵x∈[-1,16]时,f(x)≤n+1恒成立.
∴n+1≥f(x)max=4,即有n≥3.
即实数n的取值范围为[3,+∞).
点评 本题考查分段函数的图象和运用,考查不等式恒成立问题的解法,以及函数方程的转化思想的运用,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2,4} | B. | {2,4} | C. | {0,3,4} | D. | {3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
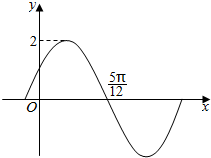 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )| A. | f(x)的最小正周期为2π | B. | f(x)的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C. | f($\frac{2π}{3}$)=-2 | D. | f(x)在[0,$\frac{π}{4}$]上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的四面体OABC中,OA=OB=OC=a,∠AOB=90°,∠BOC=∠AOC=60°,点M,N分别是AB,OC的中点,点S是MN上靠近点N的三等分点.
如图所示的四面体OABC中,OA=OB=OC=a,∠AOB=90°,∠BOC=∠AOC=60°,点M,N分别是AB,OC的中点,点S是MN上靠近点N的三等分点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$+$\frac{9{y}^{2}}{100}$=1(x≠±5) | B. | $\frac{{x}^{2}}{25}$-$\frac{9{y}^{2}}{100}$=1(x≠±5) | ||
| C. | $\frac{{y}^{2}}{25}$+$\frac{9{x}^{2}}{100}$=1(y≠±5) | D. | $\frac{{y}^{2}}{25}$-$\frac{9{x}^{2}}{100}$(y≠±5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com