
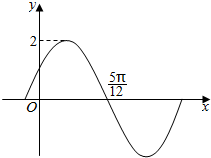
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )| A. | f(x)的最小正周期为2π | B. | f(x)的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C. | f($\frac{2π}{3}$)=-2 | D. | f(x)在[0,$\frac{π}{4}$]上是增函数 |
分析 根据函数图象的对称轴得出f(x)的对称轴,结合函数图象求出f(x)的周期和f(x)的其他对称轴.
解答 解:∵f(0)=f($\frac{π}{3}$),∴f(x)的图象在y轴右侧的第一条对称轴为x=$\frac{π}{6}$.故D错误;
∴f(x)的最小正周期T=4×($\frac{5π}{12}-\frac{π}{6}$)=π.故A错误.
∴f(x)的图象在y轴右侧的第二条对称轴为x=$\frac{π}{6}+\frac{π}{2}$=$\frac{2π}{3}$.∴f($\frac{2π}{3}$)=-1.故C正确;
f(x)的图象在y轴右侧的第三条对称轴为x=$\frac{π}{6}+π$=$\frac{7π}{6}$,故B错误.
故选C.
点评 本题考查了三角函数的图象与性质,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$ | B. | y=($\sqrt{x}$)2 | C. | y=$\frac{{x}^{2}}{x}$ | D. | y=lg10x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($-\frac{π}{2}$)<f($\sqrt{2}$)<f(e) | B. | f(e)<f($-\frac{π}{2}$)<f($\sqrt{2}$) | C. | f(e)<f($\sqrt{2}$)<f($-\frac{π}{2}$) | D. | f($\sqrt{2}$)<f($-\frac{π}{2}$)<f(e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
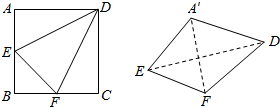 如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )
如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )| A. | 8π | B. | 6π | C. | 11π | D. | 5π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com