
分析 在等差数列中,等差数列的性质m+n=p+q,则am+an=ap+aq,那么对应的在等比数列中对应的性质是若m+n=p+q,则bmbn=bpbq.
解答 解:等差数列与等比数列的对应关系有:等差数列中的加法对应等比数列中的乘法,
等差数列中除法对应等比数列中的开方,
故此我们可以类比得到结论:${\;}^n\sqrt{{a_{n+1}}{a_{n+2}}…{a_{2n}}}={\;}^{3n}\sqrt{{a_1}{a_2}…{a_{3n}}}$.
故答案为:${\;}^n\sqrt{{a_{n+1}}{a_{n+2}}…{a_{2n}}}={\;}^{3n}\sqrt{{a_1}{a_2}…{a_{3n}}}$.
点评 本题考查类比推理,掌握类比推理的规则及类比对象的特征是解本题的关键,本题中由等差结论类比等比结论,其运算关系由加类比乘,解题的难点是找出两个对象特征的对应,作出合乎情理的类比.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 如图所示的是北京奥运会的会徽,其中的“中国印”把它分成了5个区域,现给它着色,要求相邻区域不能用同一颜色,如果只有4种颜色可供使用,那么不同的着色方法有( )种.
如图所示的是北京奥运会的会徽,其中的“中国印”把它分成了5个区域,现给它着色,要求相邻区域不能用同一颜色,如果只有4种颜色可供使用,那么不同的着色方法有( )种.| A. | 120 | B. | 72 | C. | 48 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{7}$,$\frac{3}{7}$,$\frac{6}{7}$) | B. | (-$\frac{2}{7}$,-$\frac{3}{7}$,-$\frac{6}{7}$) | ||
| C. | ($\frac{2}{7}$,-$\frac{3}{7}$,-$\frac{6}{7}$)和(-$\frac{2}{7}$,$\frac{3}{7}$,$\frac{6}{7}$) | D. | ($\frac{2}{7}$,$\frac{3}{7}$,$\frac{6}{7}$)和(-$\frac{2}{7}$,-$\frac{3}{7}$,-$\frac{6}{7}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
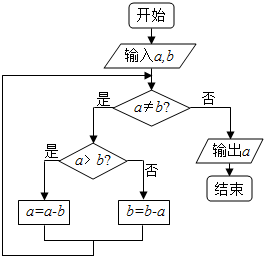
| A. | 2 | B. | 3 | C. | 7 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
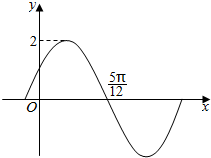 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )| A. | f(x)的最小正周期为2π | B. | f(x)的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C. | f($\frac{2π}{3}$)=-2 | D. | f(x)在[0,$\frac{π}{4}$]上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | $({\frac{1}{2},2})$ | C. | (2,+∞) | D. | (-1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com