
分析 (1)根据条件将A,B两点的坐标分别带入f(x),将B点的坐标带入g(x),便可得到关于a,b,c的三元一次方程组,解方程组即得a,b,c的值,从而求出函数f(x)和g(x)的解析式;
(2)由f(2)=0及a>b>c便可得到$-\frac{b}{2a}=1+\frac{c}{4a}$,且a>0,c<0,从而有$-\frac{1}{2}<-\frac{b}{2a}<1$,$x=-\frac{b}{2a}$是f(x)的对称轴.可设f(x)=0的另一个实根为x2,从而有x2<0且2-x2<5,进一步得到x2>-3,这样由f(m)<0便可得到-3<m<2,从而f(m+5)>0;
(3)根据条件可得$h(x)=ax+\frac{c}{x}-1$,求导数$h′(x)=\frac{a({x}^{2}-\frac{c}{a})}{{x}^{2}}$,这样便可得到h(x)在$(0,\sqrt{\frac{c}{a}})$内单调递减,在$[\sqrt{\frac{c}{a}},+∞)$内单调递增,从而可讨论$\sqrt{\frac{c}{a}}$和区间[2,4]的关系:分$\sqrt{\frac{c}{a}}≤2,2<\sqrt{\frac{c}{a}}<4$和$\sqrt{\frac{c}{a}}≥4$这几种情况,对于每种情况,根据h(x)在[2,4]上的单调性便可求出h(x)的最小值.
解答 解:(1)f(x)和g(x)的图象交于点A,B;
∴$\left\{\begin{array}{l}{9a-3b+c=3}\\{a+b+c=-1}\\{-b=-1}\end{array}\right.$;
解得a=1,b=1,c=-3;
∴f(x)=x2+x-3,g(x)=-x;
(2)证明:f(2)=4a+2b+c=0;
∵a>b>c;
∴a>0,c<0,且$-\frac{b}{a}=2+\frac{c}{2a}$;
∴$-\frac{b}{2a}=1+\frac{c}{4a}<1$,且$-\frac{b}{2a}>-\frac{1}{2}$;
即$-\frac{1}{2}<-\frac{b}{2a}<1$;
∴f(x)的对称轴在区间$(-\frac{1}{2},1)$内;
设f(x)=0的另一个根为x2,则2x2=$\frac{c}{a}<0$;
∴x2<0;
∴$2-{x}_{2}<2[2-(-\frac{1}{2})]=5$;
∴x2>-3;
∵f(m)<0;
∴-3<m<2;
∴m+5>2;
∴f(m+5)>0;
(3)b=-1,g(x)=x;
∴$h(x)=\frac{a{x}^{2}-x+c}{x}=ax+\frac{c}{x}-1$,$h′(x)=a-\frac{c}{{x}^{2}}=\frac{a({x}^{2}-\frac{c}{a})}{{x}^{2}}$;
∵a>0,c>0,x>0;
∴$x∈(0,\sqrt{\frac{c}{a}})$时,h′(x)<0,x$∈(\sqrt{\frac{c}{a}},+∞)$时,h′(x)>0;
∴h(x)在$(0,\sqrt{\frac{c}{a}})$内单调递减,在$[\sqrt{\frac{c}{a}},+∞)$内单调递增;
①若$\sqrt{\frac{c}{a}}≤2$,则h(x)在[2,4]上单调递增;
∴x=2时,h(x)取最小值2a$+\frac{c}{2}-1$;
②若$2<\sqrt{\frac{c}{a}}<4$,则x=$\sqrt{\frac{c}{a}}$时,h(x)取最小值$2\sqrt{ac}-1$;
③若$\sqrt{\frac{c}{a}}≥4$,则h(x)在[2,4]上单调递减;
∴x=4时,h(x)取最小值$4a+\frac{c}{4}-1$.
点评 考查函数图象上点的坐标和函数解析式的关系,二次函数的对称轴,韦达定理,以及要熟悉二次函数的图象,根据导数符号判断函数单调性的方法,以及根据函数单调性求函数在闭区间上的最小值的方法.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
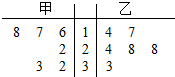 甲、乙两位运动员6场比赛的茎叶图如图所示,记甲、乙的平均成绩分别为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,下列判断正确的是( )
甲、乙两位运动员6场比赛的茎叶图如图所示,记甲、乙的平均成绩分别为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,下列判断正确的是( )| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,甲比乙成绩稳定 | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,乙比甲成绩稳定 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示的是北京奥运会的会徽,其中的“中国印”把它分成了5个区域,现给它着色,要求相邻区域不能用同一颜色,如果只有4种颜色可供使用,那么不同的着色方法有( )种.
如图所示的是北京奥运会的会徽,其中的“中国印”把它分成了5个区域,现给它着色,要求相邻区域不能用同一颜色,如果只有4种颜色可供使用,那么不同的着色方法有( )种.| A. | 120 | B. | 72 | C. | 48 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或5 | B. | -4或2 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{7}$,$\frac{3}{7}$,$\frac{6}{7}$) | B. | (-$\frac{2}{7}$,-$\frac{3}{7}$,-$\frac{6}{7}$) | ||
| C. | ($\frac{2}{7}$,-$\frac{3}{7}$,-$\frac{6}{7}$)和(-$\frac{2}{7}$,$\frac{3}{7}$,$\frac{6}{7}$) | D. | ($\frac{2}{7}$,$\frac{3}{7}$,$\frac{6}{7}$)和(-$\frac{2}{7}$,-$\frac{3}{7}$,-$\frac{6}{7}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
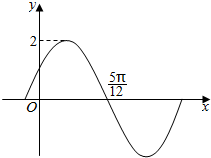 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,且f(0)=f($\frac{π}{3}$),则( )| A. | f(x)的最小正周期为2π | B. | f(x)的图象关于直线x=$\frac{5π}{6}$对称 | ||
| C. | f($\frac{2π}{3}$)=-2 | D. | f(x)在[0,$\frac{π}{4}$]上是增函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com