
【题目】轮船A从某港口O将一些物品送到正航行的轮船B上,在轮船A出发时,轮船B位于港口O北偏西30°且与O相距20海里的P处,并正以30海里/小时的航速沿正东方向匀速行驶,假设轮船A沿直线方向以V海里/小时的航速匀速行驶,经过t小时与轮船B相遇.
(1)若使相遇时轮船A航距最短,则轮船A的航行速度大小应为多少?
(2)假设轮船A的最高航行速度只能达到30海里/小时,则轮船A以多大速度及什么航行方向才能在最短时间与轮船B相遇,并说明理由.
【答案】
(1)解:设AB两船在Q处相遇,
在△OPQ中,OP=20,PQ=30t,OQ=Vt,∠OPQ=60°,
由余弦定理可得Vt= ![]() =
= ![]() ,
,
∴当t= ![]() 时,Vt取得最小值10
时,Vt取得最小值10 ![]() ,
,
此时V= ![]() =30
=30 ![]() .
.
即轮船A以30 ![]() 海里/小时的速度航行,相遇时小艇的航行距离最小
海里/小时的速度航行,相遇时小艇的航行距离最小
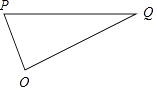
(2)解:在△POQ中,OQ=30t,
由余弦定理得:OQ2=PQ2+OP2﹣2×PQ×OPcos∠OPQ,
即(30t)2=400+900t2﹣1200tcos60°
∴600t=400
解得:t= ![]() ,∴PQ=OQ=20,
,∴PQ=OQ=20,
∴△OPQ为等边三角形,∴∠POQ=30°.
故航行方向为北偏东30°,航行速度为30海里/小时,小艇能以最短时间与轮船相遇.
【解析】(1)设AB两船在Q处相遇,根据余弦定理即可得出答案,(2)利用余弦定理计算出航行时间t,得出PQ,OQ距离,从而得出∠POQ的度数,得出航行方案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某校为了解高一年级![]() 名学生在寒假里每天阅读的平均时间(单位:小时)情况,随机抽取了
名学生在寒假里每天阅读的平均时间(单位:小时)情况,随机抽取了![]() 名学生,记录他们的阅读平均时间,将数据分成
名学生,记录他们的阅读平均时间,将数据分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并整理得到如下的频率分布直方图:
,并整理得到如下的频率分布直方图:
(![]() )求样本中阅读的平均时间为
)求样本中阅读的平均时间为![]() 内的人数.
内的人数.
(![]() )已知样本中阅读的平均时间在
)已知样本中阅读的平均时间在![]() 内的学生有
内的学生有![]() 人,现从高一年级
人,现从高一年级![]() 名学生中随机抽取一人,估计其阅读的平均时间在
名学生中随机抽取一人,估计其阅读的平均时间在![]() 内的概率.
内的概率.
(![]() )在样本中,使用分层抽样的方法,从阅读的平均时间在
)在样本中,使用分层抽样的方法,从阅读的平均时间在![]() 内的学生中抽取
内的学生中抽取![]() 人,再从这
人,再从这![]() 人中随机选取
人中随机选取![]() 人参加阅读展示,则选到的学生恰好阅读的平均时间都在
人参加阅读展示,则选到的学生恰好阅读的平均时间都在![]() 内的概率是多少?
内的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 满足Sn=2﹣an(n∈N*).数列{bn}满足(2n﹣1)bn+1﹣(2n+1)bn=0(n∈N*),且b1=1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=anbn , 求数列{cn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知锐角△ABC中,角A、B、C所对的边分别为a、b、c,若a=2,b2+c2﹣bc=4,则△ABC的面积的取值范围是( )
A.( ![]() ,
, ![]() ]
]
B.(0, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )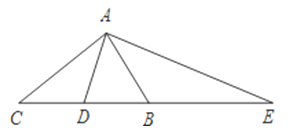
A.△AED∽△ACB
B.△AEB∽△ACD
C.△BAE∽△ACE
D.△AEC∽△DAC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)试比较BE与EF的长度关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE:EB=1:2. 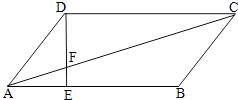
(1)求△AEF与△CDF的周长比;
(2)如果△AEF的面积等于6cm2 , 求△CDF的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)当![]() 时,写出
时,写出![]() 的通项公式(直接写出答案,无需过程);
的通项公式(直接写出答案,无需过程);
(2)求最小整数![]() ,使得当
,使得当![]() 时,
时, ![]() 是单调递增数列;
是单调递增数列;
(3)是否存在![]() 使得
使得![]() 是等比数列?若存在请求出;若不存在请说明理由.
是等比数列?若存在请求出;若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2 ![]() sin
sin ![]() ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 ![]() (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com