
分析 求出函数的导数,判断函数的导数在区间上的符号,利用导函数的符号,判断函数的单调性即可证明本题.
解答 证明:(1)函数y=xsinx+cosx,
则函数y′=sinx+xcosx-sinx=xcosx.
∵x∈($\frac{3}{2}$π,$\frac{5}{2}$π),
∴cosx>0,
∴xcosx>0,即x∈($\frac{3}{2}$π,$\frac{5}{2}$π),y′>0恒成立,
∴函数y=xsinx+cosx在区间(,)上是增函数;
(2):∵f(x)=ex+e-x
∴f′(x)=ex-e-x
令f′(x)≥0得,x≥0,
函数f(x)=ex+e-x在[0,+∞)上是增函数.
点评 本题考查函数的导数的应用,函数的单调性的判断,考查分析问题解决问题的能力.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:选择题
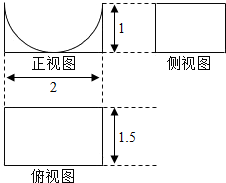
| A. | 6-$\frac{3π}{4}$ | B. | 6-$\frac{3π}{2}$ | C. | 3-$\frac{3π}{2}$ | D. | 3-$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
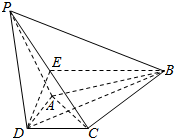 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
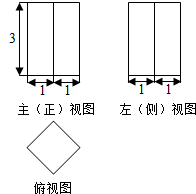
| A. | 32 | B. | 24 | C. | $4+12\sqrt{2}$ | D. | $12\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点P在椭圆C外 | B. | 点P在椭圆C内 | ||
| C. | 点P在椭圆C上 | D. | 点P与椭圆C的位置关系不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
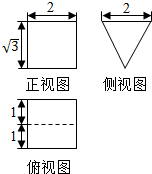
| A. | $12+\sqrt{3}$ | B. | $12+2\sqrt{3}$ | C. | $4+3\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com