
���� ��1������p1+p2+p3=1��p1��p2�Ƿ���25x2-15x+a=0������������p2=p3������p1��p2��p3��ֵ��
��2���εĿ���ȡֵΪ0��200��400��600��800�������Ӧ�ĸ��ʣ��ɵæεķֲ��У�����������ʽ����������̨���ּ��õ��������������ܺ͵�����ֵ��
��� ��12�֣�
�⣺��1 ������֪��p1+p2+p3=1��p2=p3��
��p1+2p2=1��
��p1��p2�Ƿ���20x2-15x+a=0 ����������
��p1+p2=$\frac{15}{20}$=$\frac{3}{4}$
��p1=$\frac{1}{2}$��p2=$\frac{1}{4}$��p3=$\frac{1}{4}$��
��2���εĿ���ȡֵΪ0��200��400��600��800��
P����=0��=$\frac{1}{2}��\frac{1}{2}$=$\frac{1}{4}$��P����=200��=$\frac{1}{2}$��$\frac{1}{4}$+$\frac{1}{2}��\frac{1}{4}$=$\frac{1}{4}$��
P����=400��=$\frac{1}{2}��\frac{1}{4}+\frac{1}{4}��\frac{1}{2}$=$\frac{1}{4}$��
P����=600��=$\frac{1}{4}��\frac{1}{4}$+$\frac{1}{4}��\frac{1}{4}$=$\frac{1}{8}$��
P����=800��=$\frac{1}{4}��\frac{1}{4}$=$\frac{1}{16}$
��������εķֲ���Ϊ
| �� | 0 | 200 | 400 | 600 | 800 |
| P | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{16}$ |
���� ���⿼����ʵļ��㣬������ɢ����������ķֲ�����������ȷ��������ȡֵ����������ǹؼ���


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
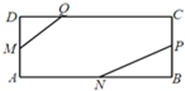 ��ͼ�ڳ�����ABCD�У���֪AB=4��BC=2��M��N��PΪ�����α��ϵ��е㣬Q�DZ�CD�ϵĵ㣬��CQ=3DQ���� $\overrightarrow{MQ}$•$\overrightarrow{NP}$��ֵ��
��ͼ�ڳ�����ABCD�У���֪AB=4��BC=2��M��N��PΪ�����α��ϵ��е㣬Q�DZ�CD�ϵĵ㣬��CQ=3DQ���� $\overrightarrow{MQ}$•$\overrightarrow{NP}$��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+$\frac{1}{a}$��b+$\frac{1}{b}$ | B�� | a+$\frac{1}{b}$��b+$\frac{1}{a}$ | C�� | $\frac{b}{a}$��$\frac{b+1}{a+1}$ | D�� | $\frac{2a-b}{a+2b}$��$\frac{a}{b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | 0 | 1 | 2 | 3 | 4 |
| P | 0.1 | 0.2 | 0.4 | 0.1 | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
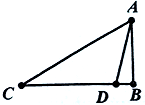 Ϊ�˲�������AB�ĸ߶ȣ���һ����C�㴦��á�ACB=30�㣬Ȼ����ǰ����20�����D����á�ADB=75�㣬��C��D��B��ͬһֱ���ϣ������AB�ĸ߶�Ϊ$5��\sqrt{3}+1��$��
Ϊ�˲�������AB�ĸ߶ȣ���һ����C�㴦��á�ACB=30�㣬Ȼ����ǰ����20�����D����á�ADB=75�㣬��C��D��B��ͬһֱ���ϣ������AB�ĸ߶�Ϊ$5��\sqrt{3}+1��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com