
| A. | x1<x2 | B. | x1>x2 | C. | ${x_1}^2<{x_2}^2$ | D. | ${x_1}^2>{x_2}^2$ |
分析 把已知函数解析式变形,由f(x1)<f(x2),得sin22x1>sin22x2,即|sin2x1|>|sin2x2|,再由x1,x2的范围可得|2x1|>|2x2|,即|x1|>|x2|,得到${{x}_{1}}^{2}>{{x}_{2}}^{2}$.
解答 解:f(x)=sin4x+cos4x=(sin2x+cos2x)2-2sin2xcos2x=$1-\frac{1}{2}si{n}^{2}2x$.
由f(x1)<f(x2),得$1-\frac{1}{2}si{n}^{2}2{x}_{1}<1-\frac{1}{2}si{n}^{2}2{x}_{2}$,
∴sin22x1>sin22x2,即|sin2x1|>|sin2x2|,
∵x1∈[-$\frac{π}{4},\frac{π}{4}$],x2∈[-$\frac{π}{4},\frac{π}{4}$],
∴2x1∈[-$\frac{π}{2}$,$\frac{π}{2}$],2x2∈[-$\frac{π}{2},\frac{π}{2}$],
由|sin2x1|>|sin2x2|,得|2x1|>|2x2|,即|x1|>|x2|,∴${{x}_{1}}^{2}>{{x}_{2}}^{2}$.
故选:D.
点评 本题考查三角函数的化简求值,考查三角函数线的应用,属中档题.


科目:高中数学 来源: 题型:选择题
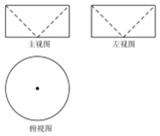 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0) | B. | [0,1] | C. | (0,1] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
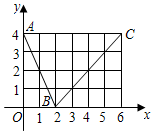 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com