Question

2．设方程x⁴+ax-4=0的各实根为x₁，x₂，…x_k（k≤4）若点（x_i，$\frac{4}{{x}_{i}}$）（i=1，2，…k）均在直线y=x的同侧，则实数a的取值范围是（　　）

• A． （4，+∞）
• B． （-∞，-6）∪（6，+∞）
• C． （6，+∞）
• D． （-∞，-4）∪（4，+∞）

Answer 1

分析 方程的根显然x≠0，从而化方程为x³+a=$\frac{4}{x}$，故原方程的实根是曲线y=x³+a与曲线y=$\frac{4}{x}$的交点的横坐标，作图辅助，从而结合图象可得$\left\{\begin{array}{l}{a＞0}\\{（-2）^{3}+a＞-2}\end{array}\right.$或$\left\{\begin{array}{l}{a＜0}\\{{2}^{3}+a＜2}\end{array}\right.$；从而解得．

解答 解：方程的根显然x≠0，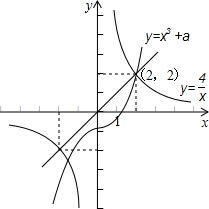
原方程可化为x³+a=$\frac{4}{x}$，
原方程的实根是曲线y=x³+a与曲线y=$\frac{4}{x}$的交点的横坐标，
而曲线y=x³+a是由曲线y=x³向上或向下平移|a|个单位而得到的，
若交点（x_i，$\frac{4}{{x}_{i}}$）（i=1，2，…，k）均在直线y=x的同侧，
因直线y=x与y=$\frac{4}{x}$交点为：（-2，-2），（2，2）；
所以结合图象可得
$\left\{\begin{array}{l}{a＞0}\\{（-2）^{3}+a＞-2}\end{array}\right.$或$\left\{\begin{array}{l}{a＜0}\\{{2}^{3}+a＜2}\end{array}\right.$；
解得，a＞6或a＜-6．
故选B．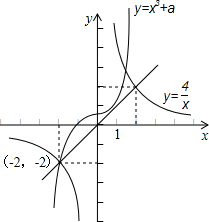

点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用，属于中档题．