函数y＝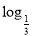
(x2－4x＋3)的单调递增区间为( )
A．(3，＋∞) B．(－∞，1)
C．(－∞，1)∪(3，＋∞) D．(0，＋∞)
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-6对数与对数函数（解析版） 题型：选择题
已知函数f(x)＝|lgx|，若a≠b，且f(a)＝f(b)，则a＋b的取值范围是( )
A．(1，＋∞) B．[1，＋∞)
C．(2，＋∞) D．[2，＋∞)
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：选择题
若函数y＝ax与y＝－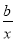
在(0，＋∞)上都是减函数，则y＝ax2＋bx在(0，＋∞)上( )
A．单调递增 B．单调递减
C．先增后减 D．先减后增
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-2函数的单调性与最值（解析版） 题型：解答题
已知函数g(x)＝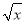
＋1，h(x)＝
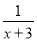，x∈(－3，a]，其中a为常数且a>0，令函数f(x)＝g(x)·h(x)．
(1)求函数f(x)的表达式，并求其定义域；
(2)当a＝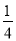
时，求函数f(x)的值域．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-1函数的概念、定义域和值域（解析版） 题型：填空题
对a，b∈R，记min{a，b}＝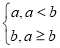
，函数f(x)＝min{
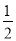x，－|x－1|＋2}(x∈R)的最大值为________．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-1函数的概念、定义域和值域（解析版） 题型：选择题
设集合A＝[0，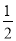
)，B＝[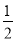
，1]，函数f(x)＝
，若x0∈A，且f[f(x0)]∈A，则x0的取值范围是( )
A．(0，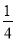
] B．(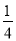
，
)
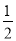C．(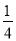
，
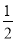] D．[0，
]
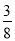查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：10-8n次独立重复实验与二项分布（解析版） 题型：填空题
已知数列{an}是单调递增的等差数列，从a1，a2，a3，a4，a5，a6，a7中取走任意三项，则剩下四项依然构成单调递增的等差数列的概率是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
u与u＝x2－4x＋3的复合函数．
(x2－4x＋3)的定义域为(－∞，1)∪(3，＋∞)．
u在(0，＋∞)上是减函数，
(x2－4x＋3)的单调递减区间为(3，＋∞)，单调递增区间为(－∞，1)．
在(－2，＋∞)上为增函数，则a的取值范围是________．
ex(sinx＋cosx)在区间[0，
]上的值域为( )