
分析 由条件利用两角和差的余弦公式求得cos($\frac{α}{2}$+$\frac{π}{4}$)=$\frac{1}{2}$,再利用诱导公式、二倍角公式求得sinα=-cos(α+$\frac{π}{2}$) 的值.
解答 解:∵sin$\frac{α}{2}$-cos$\frac{α}{2}$=-$\frac{\sqrt{2}}{2}$,∴$\frac{\sqrt{2}}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{2}}{2}$sin$\frac{α}{2}$=cos($\frac{α}{2}$+$\frac{π}{4}$)=$\frac{1}{2}$,
则sinα=-cos(α+$\frac{π}{2}$)=-[2${cos}^{2}(\frac{α}{2}+\frac{π}{4})$-1]=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查两角和差的余弦公式、诱导公式、二倍角公式的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
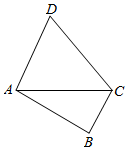 如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.
如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com