
| A. | -$\frac{15}{4}$ | B. | -$\frac{3}{8}$ | C. | $\frac{15}{4}$ | D. | -1 |
分析 根据二项展开式的通项公式,令展开式的含x项的指数为1,即可求出展开式中x项的系数.
解答 解:($\frac{{\sqrt{x}}}{2}$-$\frac{2}{{\sqrt{x}}}$)4的二项展开式中,通项公式为
Tr+1=(-1)r•${C}_{4}^{r}$•($\frac{\sqrt{x}}{2}$)4-r•($\frac{2}{\sqrt{x}}$)r=(-1)r•${C}_{4}^{r}$•22r-4•x2-r;
令2-r=1,可得r=1,
∴展开式中x项的系数是(-1)•${C}_{4}^{1}$•2-2=-1.
故选:D.
点评 本题考查了二项式展开式的通项公式的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
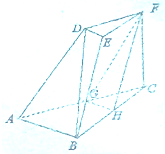 如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥2 | B. | m≤2 | C. | m>2 | D. | -2<m<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{{\sqrt{3}}}{3}$,$\sqrt{3}$] | B. | [1,$\sqrt{3}$] | C. | [1,+∞) | D. | (-∞,-$\sqrt{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com