

| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �ڢ��У�������A-BCD��������ֵΪ$\frac{24}{5}$���ڢ��У�����A-BCD�����ı����Ϊ25�У��ڢ��У�����AF��CF���õ�EF��AC������DE��BE���á�ACD�ա�ACB����DE=BE���Ӷ�EF��BD���ڢ��У���CΪԭ��CB��CD����ֱ�߷ֱ�Ϊx��y�ᣬ�����������������Եõ�ֱ��AB��CD���ɽǵ�����ֵΪ$\frac{16}{25}$���ڢ��У��������A-BD-C�Ĵ�СΪ60��ʱ��AC=$\frac{\sqrt{193}}{5}$��
��� �⣺��������ABCD������ֵΪ�����滥�ഹֱ��
������A-BCD��������ֵΪ$\frac{1}{3}��\frac{1}{2}��3��4��\frac{12}{5}$=$\frac{24}{5}$���ʢٲ���ȷ��
������A-BCD�����İ뾶Ϊ$\frac{5}{2}$��
��������A-BCD�����ı����Ϊ4$�С�\frac{25}{4}=25��$���ʢ���ȷ��
����E��F�ֱ�Ϊ��AC��BD���е㣬����AF��CF��AF=CF��
���ݵ������������ߺ�һ�õ�EF��AC��
����DE��BE���á�ACD�ա�ACB��
�õ�DE=BE������EF��BD���ʢ���ȷ��
�ܵ������A-BD-CΪֱ�����ʱ����CΪԭ��CB��CD����ֱ�߷ֱ�Ϊx��y�ᣬ
�������������������Եõ�ֱ��AB��CD���ɽǵ�����ֵΪ$\frac{16}{25}$���ʢ���ȷ��
����ֱ��������ABD�У�AB=4��AD=3��BD=5��
��AE��BD��CF��BD����AE=CF=$\frac{12}{5}$��DE=BF=$\frac{9}{5}$��
ͬ��ֱ��������ABC�У���EF=BD-DE-BF=$\frac{7}{5}$��
��ƽ��ABD�ڣ���F��FH��AE����FH=AE������AH�����ı���AEFHΪ���Σ�
��AH=EF=$\frac{7}{5}$��AH��EF��
FH��DB����CF��DB��
���С�CFHΪ�����C-BD-A��ƽ��ǣ���Ϊ60�㣬
��CH=CF=$\frac{12}{5}$��
��BD��ƽ��CFH���õ�BD��CH������AH��CH��
��AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=$\frac{\sqrt{193}}{5}$���ʢݴ���
��ѡ��C��
���� ���⿼��������ٵ��жϣ����е��⣬����ʱҪ�������⣬ע��ռ�˼ά������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{3}$ | B�� | $-\frac{4}{3}$ | C�� | $\frac{3}{4}$ | D�� | $-\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a-1��2��a+2�� | B�� | ��a+1��2��a+2�� | C�� | ��a-1����a+1����a-2�� | D�� | ��a-1��2��a-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
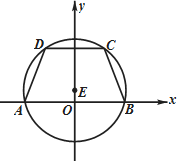 ��ͼ��ʾ����������ABCD�ĵױ�AB��x���ϣ�����A�붥��B����ԭ��O�Գƣ��ҵױ�AB��CD�ij��ֱ�Ϊ6��$2\sqrt{6}$����Ϊ3��
��ͼ��ʾ����������ABCD�ĵױ�AB��x���ϣ�����A�붥��B����ԭ��O�Գƣ��ҵױ�AB��CD�ij��ֱ�Ϊ6��$2\sqrt{6}$����Ϊ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com