
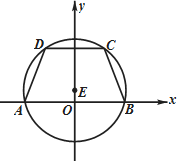
 如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和$2\sqrt{6}$,高为3.
如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和$2\sqrt{6}$,高为3.分析 (Ⅰ)确定四个顶点的坐标,根据对称性判断出E在y轴上,设其坐标,利用两点间的距离公式建立等式求得E的坐标和半径,则圆的方程可得.
(Ⅱ)设出P的坐标,表示出M的坐标代入圆E的方程,进而求得P的轨迹方程.
解答 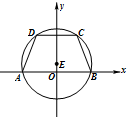 解:(Ⅰ)设E(0,b),
解:(Ⅰ)设E(0,b),
由已知可得:$A(-3,0),B(3,0),C(\sqrt{6},3),D(-\sqrt{6},3)$,(2分)
由|EB|=|EC|得:${(3-0)^2}+{(0-b)^2}={(\sqrt{6}-0)^2}+{(3-b)^2}⇒b=1$,(4分)
∴圆E的圆心为E(0,1),半径为$r=\sqrt{10}$,
∴圆E的方程为:x2+(y-1)2=10.(6分)
(Ⅱ)设P(x,y),M(x0,y0),(7分)
∵P为线段MN的中点,∴$\left\{\begin{array}{l}\frac{{5+{x_0}}}{2}=x\\ \frac{{2+{y_0}}}{2}=y\end{array}\right.⇒\left\{\begin{array}{l}{x_0}=2x-5\\{y_0}=2y-2\end{array}\right.$,(9分)
代入点${(2x-5)^2}+{(2y-3)^2}=10⇒{(x-\frac{5}{2})^2}+{(y-\frac{3}{2})^2}=\frac{5}{2}$所在圆的方程得:${(2x-5)^2}+{(2y-3)^2}=10⇒{(x-\frac{5}{2})^2}+{(y-\frac{3}{2})^2}=\frac{5}{2}$,(11分)
∴点${(x-\frac{5}{2})^2}+{(y-\frac{3}{2})^2}=\frac{5}{2}$的轨迹方程为${(x-\frac{5}{2})^2}+{(y-\frac{3}{2})^2}=\frac{5}{2}$.(12分)
点评 本题主要考查了直线与圆的方程的应用.求圆的方程,一般是确定圆心和半径.解决轨迹方程的问题的步骤先设点,求得变量x和y的关系即可.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
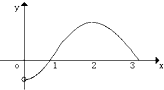 已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(-x)•x>0的解集是( )
已知函数f(x)是定义在(-3,0)∪(0,3)上的偶函数,当0<x<3时,f(x)的图象如图所示,则不等式f(-x)•x>0的解集是( )| A. | (-1,0)∪(0,1) | B. | (-3,-1)∪(1,3) | C. | (-3,-1)∪(0,1) | D. | (-1,0)∪(1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com