
分析 以CD为x轴,CD的中垂线为y轴建立平面直角坐标系,求出对应点的坐标,根据向量数量积的坐标公式进行计算即可.
解答 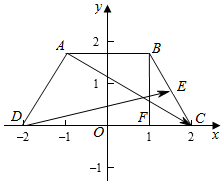 解:以CD为x轴,CD的中垂线为y轴建立平面直角坐标系,
解:以CD为x轴,CD的中垂线为y轴建立平面直角坐标系,
∵AB=BC=2,∠ABC=120°,
∴过B作FB⊥CD,
则FC=1,BF=$\sqrt{3}$,即OC=2,CD=4,
∴A(-1,$\sqrt{3}$),C(2,0),B(1,$\sqrt{3}$),
D(-2,0),E($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
则$\overrightarrow{AC}$=(3,-$\sqrt{3}$),$\overrightarrow{DE}$=($\frac{7}{2}$,$\frac{\sqrt{3}}{2}$),
则$\overrightarrow{AC}$•$\overrightarrow{DE}$=(3,-$\sqrt{3}$)•($\frac{7}{2}$,$\frac{\sqrt{3}}{2}$)=$\frac{21}{2}$-$\frac{3}{2}$=9,
故答案为:9.
点评 本题考查了平面向量的数量积运算,建立坐标系转化为坐标运算是解题关键,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-1,2) | C. | (2,+∞) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 双曲线 | C. | 抛物线 | D. | 椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
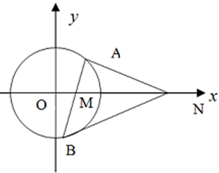 已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方
已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com