
| A. | -1或$-\frac{7}{4}$ | B. | -1或$\frac{7}{4}$ | C. | 1或-$\frac{7}{4}$ | D. | 1或$\frac{7}{4}$ |
分析 根据条件可先求出向量$2\overrightarrow{a}+\overrightarrow{b}$和$\overrightarrow{a}-\overrightarrow{b}$的坐标,根据$(2\overrightarrow{a}+\overrightarrow{b})⊥(\overrightarrow{a}-\overrightarrow{b})$即可得到$(2\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})=0$,进行数量积的坐标运算即可得到关于λ的方程,解出λ即可.
解答 解:$2\overrightarrow{a}+\overrightarrow{b}=(2λ+1,2λ-2),\overrightarrow{a}-\overrightarrow{b}=(λ-1,λ-4)$;
∵$(2\overrightarrow{a}+\overrightarrow{b})⊥(\overrightarrow{a}-\overrightarrow{b})$;
∴$(2\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})=0$,即(2λ+1)(λ-1)+(2λ-2)(λ-4)=0;
整理得,4λ2-11λ+7=0;
解得,λ=1,或$\frac{7}{4}$.
故选D.
点评 考查向量坐标的加法、减法和数乘运算,向量垂直的充要条件,以及向量数量积的坐标运算.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:选择题
| A. | 960 | B. | -160 | C. | -560 | D. | -960 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {0,1} | C. | {2} | D. | {0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
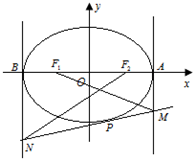 如图,已知椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上任意一点P(异于顶点)处的切线与该椭圆在长轴顶点A,B处的切线分别交于点M,N,该椭圆的左,右焦点分别是F1,F2,直线MF1,NF2的斜率分别是k1,k2.
如图,已知椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上任意一点P(异于顶点)处的切线与该椭圆在长轴顶点A,B处的切线分别交于点M,N,该椭圆的左,右焦点分别是F1,F2,直线MF1,NF2的斜率分别是k1,k2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com