
(本小题满分14分)设函数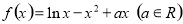 .
.
(1)求函数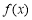 的单调区间;
的单调区间;
(2)已知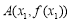 ,
,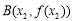 (
(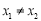 )是函数
)是函数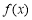 在
在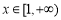 的图象上的任意两点,且满足
的图象上的任意两点,且满足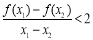 ,求a的最大值;
,求a的最大值;
(3)设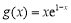 ,若对于任意给定的
,若对于任意给定的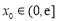 ,方程
,方程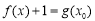 在
在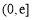 内有两个不同的实数根,求a的取值范围.(其中
内有两个不同的实数根,求a的取值范围.(其中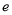 是自然对数的底数)
是自然对数的底数)
(1)函数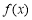 的单调递增区间是
的单调递增区间是 ;递减区间是
;递减区间是 ;(2)3
;(2)3
(3) .
.
【解析】
试题分析:(1)函数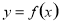 在某个区间内可导,则若
在某个区间内可导,则若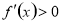 ,则
,则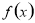 在这个区间内单调递增,若
在这个区间内单调递增,若 ,则
,则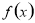 在这个区间内单调递减;(2)利用导数方法证明不等式
在这个区间内单调递减;(2)利用导数方法证明不等式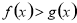 在区间
在区间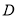 上恒成立的基本方法是构造函数
上恒成立的基本方法是构造函数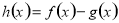 ,然后根据函数的单调性,或者函数的最值证明函数
,然后根据函数的单调性,或者函数的最值证明函数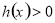 ,其中一个重要的技巧就是找到函数
,其中一个重要的技巧就是找到函数 在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式;(3))对于恒成立的问题,常用到两个结论:(1)
在什么地方可以等于零,这往往就是解决问题的一个突破口,观察式子的特点,找到特点证明不等式;(3))对于恒成立的问题,常用到两个结论:(1) ,(2)
,(2)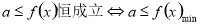 ,(4)解决含有参数的单调性的问题,要注意分类讨论和数形结合的思想.
,(4)解决含有参数的单调性的问题,要注意分类讨论和数形结合的思想.
试题解析:(1) , 1分
, 1分
由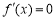 ,得
,得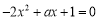 ,该方程的判别式△=
,该方程的判别式△=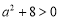 ,
,
可知方程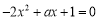 有两个实数根
有两个实数根 ,又
,又 ,故取
,故取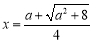 ,
,
当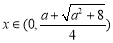 时,
时,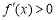 ,函数
,函数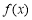 单调递增;当
单调递增;当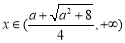 时,
时,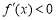 ,函数
,函数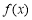 单调递减.
单调递减.
则函数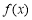 的单调递增区间是
的单调递增区间是 ;递减区间是
;递减区间是 . 3分
. 3分
(2)不妨设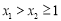 ,不等式
,不等式 转化为
转化为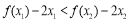 ,
,
令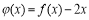 ,可知函数
,可知函数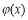 在区间
在区间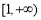 上单调递减,故
上单调递减,故 恒成立,
恒成立,
故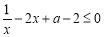 恒成立,即
恒成立,即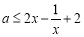 恒成立. 5分
恒成立. 5分
当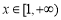 时,函数
时,函数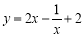 单调递增,故当
单调递增,故当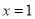 时,函数
时,函数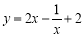 取得最小值3,则实数
取得最小值3,则实数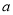 的取值范围是
的取值范围是 ,则实数
,则实数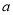 的最大值为3. 7分
的最大值为3. 7分
(3) ,当
,当 时,
时,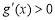 ,
, 是增函数;当
是增函数;当 时,
时,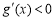 ,
, 是减函数.可得函数
是减函数.可得函数 在区间
在区间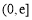 的值域为
的值域为 . 9分
. 9分
令 ,则
,则 ,
,
由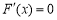 ,结合(1)可知,方程
,结合(1)可知,方程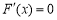 在
在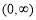 上有一个实数根
上有一个实数根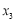 ,若
,若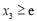 ,则
,则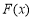 在
在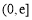 上单调递增,不合题意,可知
上单调递增,不合题意,可知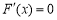 在
在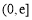 有唯一的解
有唯一的解 ,且
,且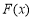 在
在 上单调递增;在
上单调递增;在 上单调递减. 10分
上单调递减. 10分
因为
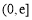 ,方程
,方程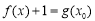 在
在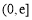 内有两个不同的实数根,所以
内有两个不同的实数根,所以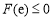 ,且
,且 . 11分
. 11分
由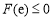 ,即
,即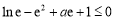 ,解得
,解得 .
.
由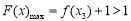 ,即
,即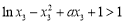 ,
, ,
,
因为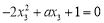 ,所以
,所以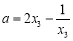 ,代入
,代入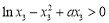 ,得
,得 ,
,
令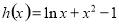 ,可知函数
,可知函数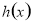 在
在 上单调递增,而
上单调递增,而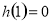 ,则
,则 ,
,
所以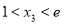 ,而
,而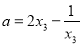 在
在 时单调递增,可得
时单调递增,可得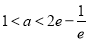 ,
,
综上所述,实数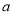 的取值范围是
的取值范围是 14分.
14分.
考点:1、利用导数求函数的单调区间;2、利用导数求函数的最值;3、方程根的个数.


科目:高中数学 来源:2015届天津市高三上学期零月月考理科数学试卷(解析版) 题型:填空题
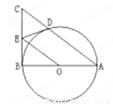
以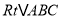 的直角边AB为径作圆O,圆O与斜边AC交于D,过D作圆O的切线与BC交于E,若BC=3,AB=4,则OE= .
的直角边AB为径作圆O,圆O与斜边AC交于D,过D作圆O的切线与BC交于E,若BC=3,AB=4,则OE= .
查看答案和解析>>
科目:高中数学 来源:2015届天津市高三上学期零月月考文科数学试卷(解析版) 题型:填空题
已知圆C的圆心与抛物线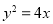 的焦点关于直线y=x对称,直线4x-3y-2=0与圆C相交于A,B两点,且
的焦点关于直线y=x对称,直线4x-3y-2=0与圆C相交于A,B两点,且 ,则圆C的标准方程为: .
,则圆C的标准方程为: .
查看答案和解析>>
科目:高中数学 来源:2015届天津市高三上学期零月月考文科数学试卷(解析版) 题型:选择题
已知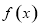 是定义在
是定义在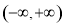 上的偶函数,且在
上的偶函数,且在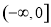 上是增函数,设
上是增函数,设
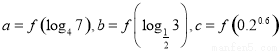 ,则
,则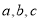 的大小关系是( )
的大小关系是( )
A.c<b<a B.b<c<a C.b<a<c D.a<b<c
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
在各项均为正数的等比数列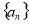 中,
中,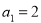 ,且
,且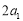 ,
,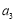 ,
,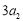 成等差数列.
成等差数列.
(1)求等比数列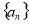 的通项公式;
的通项公式;
(2)若数列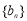 满足
满足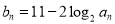 ,求数列
,求数列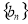 的前n项和
的前n项和 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试理科数学试卷(解析版) 题型:选择题
已知函数 ,
, ,则下列不等式正确的是
,则下列不等式正确的是
(A)x1>x2 (B)x1<x2
(C)x1+x2<0 (D)x1+x2>0
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试文科数学试卷(解析版) 题型:填空题
△ABC中,角A,B,C的对边分别为a,b,c,已知b=8,c=6,a=4,D为边BC的中点,则|AD|=___________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试文科数学试卷(解析版) 题型:填空题
已知函数f (x)= , 则f (
, 则f (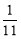 )+f (
)+f ( )+f (
)+f (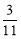 )+…+f (
)+…+f (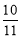 )=________.
)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com