练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．有一个7人学习合作小组，从中选取4人发言，要求其中组长和副组长至少有一人参加，若组长和副组长同时参加，则他们发言时顺序不能相邻，那么不同的发言顺序有（　　）
    A．720种B．600种C．360种D．300种

    分析 根据题意，分2种情况讨论，①只有甲乙其中一人参加，②甲乙两人都参加，分别求出每一种情况下的情况数目，再由加法原理计算可得答案．

    解答 解：根据题意，分2种情况讨论，
    ①、若甲乙其中一人参加，需要从剩余5人中选取3人，
    从甲乙中任取1人，有2种情况，
    在剩余5人中任取3人，有C53=10种情况，
    将选取的4人，进行全排列，有A44=24种情况，
    则此时有2×10×24=480种情况；
    ②、若甲乙两人都参加，
    需要从剩余5人中选取2人，有C52=10种选法，
    将甲乙和选出的2人，进行全排列，有A44=24种情况，
    则甲乙都参加有10×24=240种情况，
    其中甲乙相邻的有C52A44A22A33=120种情况；
    则甲乙两人都参加且不相邻的情况有240-120=120种；
    则不同的发言顺序种数480+120=600种，
    故选：B．

    点评 本题考查排列、组合知识，此类问题需要注意常见问题的处理方法，如相邻问题用捆绑法等，本题的关键是根据题意正确进行分类讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．设a∈R，则“a=1”是“直线ax+y-1=0与直线x+ay+5=0平行”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．函数y=cos2（x+$\frac{π}{2}$）的单调递增区间（　　）
    A．（kπ，kπ+$\frac{π}{2}$）k∈ZB．（kπ+$\frac{π}{2}$，kπ+π）k∈ZC．（2kπ，2kπ+π）k∈ZD．（2kπ，2kπ+2π）k∈Z

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，a为双曲线虚轴的一个顶点，过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B，若$\overrightarrow{AB}$=（$\sqrt{2}$-1）$\overrightarrow{AF}$，则此双曲线的离心率是（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2$\sqrt{2}$D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设集合A={x∈N|y=ln（2-x）}，B={x|x（x-1）≤0}，则A∩B=（　　）
    A．{x|x≥1}B．{x|1≤x＜2}C．{1}D．{0，1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=$\frac{x-1}{lnx}$．
    （Ⅰ）试判断函数y=f（x）在（1，+∞）上的单调性；
    （Ⅱ）令an+1=f（an）（n∈N•），若a1=$\sqrt{e}$，求证2nlnan≥1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

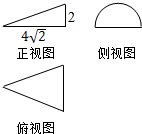    19．一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（　　）
    A．$\frac{8\sqrt{2}π}{3}$B．$\frac{16\sqrt{2}π}{3}$C．4$\sqrt{2}π$D．8$\sqrt{2}π$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

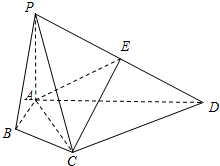    16．在四棱锥P-ABCD中，PA⊥平面ABCD，E是PD的中点，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，AC=AP．
    （Ⅰ）求证：CE∥平面PAB；
    （Ⅱ）求证：PC⊥AE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．关于x的不等式（ax+b）（x-2）＞0（b＞0）的解集为A，记满足（1，2）⊆A的有序实数对（a，b）构成集合N，若向集合M={（a，b）|-1＜a＜0，0＜b＜2}所在平面区域内投掷一质点，质点等可能地落在M内任意一点，则该质点恰好落在集合N所在区域内的概率为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{1}{8}$D．$\frac{1}{6}$

    查看答案和解析>>

    同步练习册答案