
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | $\frac{\sqrt{3}+1}{2}$ |
分析 根据条件可知点D在线段AB上,从而可作出图形,并过D分别作AC,BC的垂线DE,DF,可设AC=BC=a,从而可根据条件得到CE=ta,CF=(1-t)a,这样在Rt△CDE和Rt△CDF中,由余弦函数的定义即可得到$\frac{ta}{\frac{1}{2}}=\frac{(1-t)a}{\frac{\sqrt{3}}{2}}$,从而可解出t的值.
解答 解:如图,根据题意知,D在线段AB上,过D作DE⊥AC,垂足为E,作DF⊥BC,垂足为F;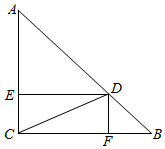
若设AC=BC=a,则由$\overrightarrow{CD}=t\overrightarrow{CA}+(1-t)\overrightarrow{CB}$得,CE=ta,CF=(1-t)a;
根据题意,∠ACD=60°,∠DCF=30°;
∴$\frac{CE}{cos60°}=\frac{CF}{cos30°}$;
即$\frac{ta}{\frac{1}{2}}=\frac{(1-t)a}{\frac{\sqrt{3}}{2}}$;
解得$t=\frac{\sqrt{3}-1}{2}$.
故选:A.
点评 考查当满足$\overrightarrow{CD}=t\overrightarrow{CA}+(1-t)\overrightarrow{CB}$时,便说明D,A,B三点共线,以及向量加法的平行四边形法则,平面向量基本定理,余弦函数的定义.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | 10 | C. | 12 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
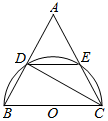 已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.
已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 23 | C. | 22 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ | B. | ?m∈[0,1],则$x+\frac{1}{x}≥{2^m}$ | ||
| C. | ?m∈(-∞,0)∪(1,+∞),则$x+\frac{1}{x}≥{2^m}$ | D. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com