
分析 (1)由已知向量的坐标结合数量积公式得到f(x),再由倍角公式及两角和的正弦化简得答案;
(2)由f(α-$\frac{π}{3}$)=2列式求得cos($2α+\frac{π}{6}$)=-$\frac{1}{2}$,由α得范围求得$2α+\frac{π}{6}$的范围,再由平方关系求得sin(2α+$\frac{π}{6}$)的值.
解答 解:(1)∵$\overrightarrow{a}$=(2cos2x,$\sqrt{3}$),$\overrightarrow{b}$=(1,sin2x),
∴f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=2cos2x+$\sqrt{3}sin2x$=$\sqrt{3}sin2x+cos2x+1$=$2sin(2x+\frac{π}{6})+1$,
由$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$,得$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6},k∈Z$.
∴函数f(x)的单调增区间为[$kπ-\frac{π}{3}$,$kπ+\frac{π}{6}$],k∈Z;
(2)f(α-$\frac{π}{3}$)=2sin(2$α-\frac{2π}{3}+\frac{π}{3}$)+1=2sin(2α-$\frac{π}{3}$)+1=2,
∴sin(2α-$\frac{π}{3}$)=$\frac{1}{2}$,
则sin($\frac{π}{3}-2α$)=-$\frac{1}{2}$,即cos($2α+\frac{π}{6}$)=-$\frac{1}{2}$,
∵α∈[$\frac{π}{2}$,π],∴$2α+\frac{π}{6}$∈[$\frac{7π}{6},\frac{13π}{6}$],
则sin(2α+$\frac{π}{6}$)=-$\sqrt{1-co{s}^{2}(2α+\frac{π}{6})}=-\sqrt{1-(-\frac{1}{2})^{2}}$=$-\frac{\sqrt{3}}{2}$.
点评 本题考查平面向量的数量积运算,考查了三角函数的倍角公式的应用,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{6}$$+\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{4}$+y2=1 | C. | $\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{6}$=1 | D. | x2$+\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 有效 | 无效 | 合计 | |
| 使用方案A组 | 96 | 120 | |
| 使用方案B组 | 72 | ||
| 合计 | 32 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
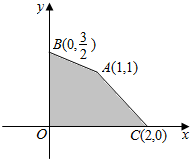 给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.
给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com