
【题目】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A、B、C三地位于同一水平面上,在C处进行该仪器的垂直弹射,观测点A、B两地相距100米,∠BAC=60°,在A地听到弹射声音的时间比在B地晚![]()
秒. A地测得该仪器弹至最高点H时的仰角为30°.
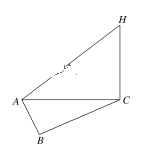
(1)求A、C两地的距离;
(2)求该仪器的垂直弹射高度CH.(声音的传播速度为340米/秒)
【答案】(1)420;(2)![]()
【解析】分析:(1)利用在A地听到弹射声音的时间比B地晚k秒,求出BC,利用余弦定理,即可求得结论;
(2)在△ACH中,AC=420,∠CAH=30°,利用正弦函数,可得结论.
详解:
(1)由题意,设AC=x,
则BC=x-![]() =x-40.
=x-40.
在△ABC中,由余弦定理,得
BC2=BA2+AC2-2BAACcos∠BAC,
即(x-40)2=10 000+x2-100x,解得x=420.
∴A、C两地间的距离为420m.
(2)在Rt△ACH中,AC=420,∠CAH=30°,
所以CH=ACtan∠CAH=140.
答: 该仪器的垂直弹射高度CH为140米.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】如图,某公园摩天轮的半径为![]() ,圆心距地面的高度为
,圆心距地面的高度为![]() ,摩天轮做匀速转动,每
,摩天轮做匀速转动,每![]() 转一圈,摩天轮上的点
转一圈,摩天轮上的点![]() 的起始位置在最低点处.
的起始位置在最低点处.
(1)已知在时刻![]() 时
时![]() 距离地面的高度
距离地面的高度![]() ,(其中
,(其中![]() ),求
),求![]() 时
时![]() 距离地面的高度;
距离地面的高度;
(2)当离地面![]() 以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?
以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试,现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
,![]() ,…,
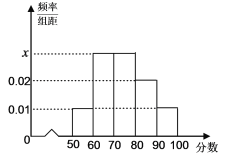
,…,![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
(Ⅰ)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
的值,并估计所抽取的50名学生成绩的中位数(用分数表示);
(Ⅱ)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取2人参加这次考试的考后分析会,试求![]() 组中至少有1人被抽到的概率.
组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的对称轴方程;
的对称轴方程;
(2)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() △三个内角
△三个内角![]() ,
, ![]() ,
, ![]() 的对边,
的对边, ![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求证二面角A1﹣BC1﹣B1的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.点E是CD边的中点,点F,G分别在线段AB,BC上,且AF=2FB,CG=2GB.

(1)证明:PE⊥FG;
(2)求二面角PADC的正切值;
(3)求直线PA与直线FG所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com