
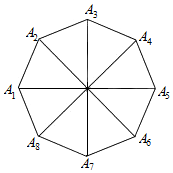
 如图所示,中心为O的正八边形A1A2…A7A8中,$\overrightarrow{{a}_{i}}$=$\overrightarrow{{A}_{i}{A}_{i+1}}$(i=1,2,…,7),$\overrightarrow{{b}_{j}}$=$\overrightarrow{O{A}_{j}}$(j=1,2,…,8),试化简$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$.
如图所示,中心为O的正八边形A1A2…A7A8中,$\overrightarrow{{a}_{i}}$=$\overrightarrow{{A}_{i}{A}_{i+1}}$(i=1,2,…,7),$\overrightarrow{{b}_{j}}$=$\overrightarrow{O{A}_{j}}$(j=1,2,…,8),试化简$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$. 分析 根据向量的三角形法则和正八边形的性质化简.
解答 解:∵$\overrightarrow{{a}_{2}}$+$\overrightarrow{{b}_{7}}$=$\overrightarrow{{A}_{2}{A}_{3}}$+$\overrightarrow{O{A}_{7}}$=$\overrightarrow{{A}_{2}{A}_{3}}$+$\overrightarrow{{A}_{3}O}$=$\overrightarrow{{A}_{2}O}$,$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{5}}$=$\overrightarrow{{A}_{5}{A}_{6}}$+$\overrightarrow{O{A}_{5}}$=$\overrightarrow{O{A}_{6}}$=$\overrightarrow{{A}_{2}O}$,
∴$\overrightarrow{{a}_{2}}$+$\overrightarrow{{b}_{7}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{5}}$=$\overrightarrow{0}$,
∴$\overrightarrow{{a}_{2}}$+$\overrightarrow{{a}_{5}}$+$\overrightarrow{{b}_{2}}$+$\overrightarrow{{b}_{5}}$+$\overrightarrow{{b}_{7}}$=$\overrightarrow{{b}_{2}}$.
点评 本题考查了平面向量运算的三角形法则,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 194种 | B. | 193种 | C. | 192种 | D. | 191种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{9}$ | B. | 0 | C. | -$\frac{5}{18}$ | D. | -$\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | b | |
| 乙班 | c | 30 | |
| 总计 | 105 |
| P(K2≥K0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
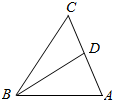 如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.
如图,在△ABC中,已知AB=3,BC=4,∠ABC=60°,BD为AC边上的中线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | t | 6.5 | 7.0 |
| A. | 5.5 | B. | 5.0 | C. | 4.5 | D. | 4.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com