
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
分析 (1)根据简单随机抽样的定义即可得到结论,
(2)①根据数学成绩优秀率是30%,构造关于a的方程,解方程可得a值,进而根据抽取样本容量为100,可得b值;
②求出满足a≥10,b≥8的基本事件总数及满足数学成绩优秀的人数比及格的人数少的基本事件个数,代入古典概型概率计算公式,可得答案
解答 解:(1)根据图表数据第一个数为785,依次为667,199,507,175,
(2)①$\frac{7+9+a}{100}$=30%,
∴a=14;
b=100-30-(20+18+4)-(5+6)=17
②a+b=100-(7+20+5)-(9+18+6)-4=31
因为a≥10,b≥8,
所以a,b的搭配:
(10,21),(11,20),(12,19),(13,18),(14,17),(15,16),(16,15),
(17,14),(18,13),(19,12),(20,11),(21,10),(22,9),(23,8),
共有14种,
设a≥10,b≥8时,数学成绩优秀的人数比及格的人数少为事件A,
事件A包括:((10,21),(11,20),(12,19),(13,18),(14,17),(15,16),
共6个基本事件;
∴数学成绩优秀的人数比及格的人数少的概率p=$\frac{6}{14}$=$\frac{3}{7}$.
点评 本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2+i | B. | 1+2i | C. | -1+2i | D. | -2+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )| A. | $\sqrt{22}$ | B. | $\sqrt{21}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.6 | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
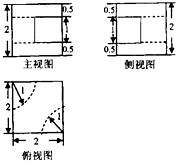
| A. | 8-$\frac{π}{6}$ | B. | 8-$\frac{π}{4}$ | C. | 8-$\frac{π}{3}$ | D. | 8-$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com