
分析 由S8>S9,且S9=S8+a9,得到a9<0,由S8>S7,S8=S7+a8,得到a8>0,从而d=a9-a8<0;由S9>S7,得到a8+a9>0,得到S16=8(a8+a9)>0;由a8>0,a9<0,得数列{Sn}中的最大项为S8,;由8(a8+a9)>0,得|a8|>|a9|.
解答 解:∵S8>S9,且S9=S8+a9,
∴S8>S8+a9,即a9<0,
又S8>S7,S8=S7+a8,
∴S7+a8>S7,即a8>0,
∴d=a9-a8<0,故①为真命题;
∵S9>S7,S9=S7+a8+a9,
∴S7+a8+a9>S7,即a8+a9>0,
又∵a1+a15=2a8,
∴S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=15a8>0,
又∵a1+a16=a8+a9,
∴S16=$\frac{16({a}_{1}+{a}_{16})}{2}$=8(a8+a9)>0,故②错误;
又a1+a17=2a9,
∴S17=$\frac{17({a}_{1}+{a}_{17})}{2}$=17a9<0,
∵a8>0,a9<0,∴数列{Sn}中的最大项为S8,故③错误;
∵8(a8+a9)>0,∴|a8|>|a9|,故④正确;
故答案为:①④.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
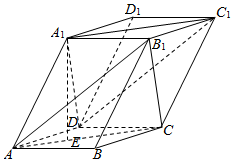 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [10,12) | B. | [16,20] | C. | [8,12] | D. | [12,14) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,-7) | B. | (4,7) | C. | (4,-1) | D. | (4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com