
【题目】已知函数![]()
(1)若函数![]() 在区间
在区间![]() 上单调递减,求实数a的取值范围;
上单调递减,求实数a的取值范围;
(2)当![]() ,(
,(![]() )时,求证:
)时,求证:![]() ;
;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求证:
,求证:![]() (e为自然对数的底数)
(e为自然对数的底数)
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)由题意可知![]() 在
在![]() 上恒成立,通过参变分离可知
上恒成立,通过参变分离可知![]() 恒成立,结合导数可求出
恒成立,结合导数可求出![]() 的最大值,从而可求出实数a的取值范围.
的最大值,从而可求出实数a的取值范围.
(2)由(1)可知![]() ,从而可知
,从而可知![]() ,结合累加法可知
,结合累加法可知![]() ,进而可证出
,进而可证出![]() .
.
(3)由题意可知![]() 有两个相异实根
有两个相异实根![]() ,
,![]() ,进而可知
,进而可知![]() ,结合导数证明
,结合导数证明![]() 在
在![]() 成立,从而可知
成立,从而可知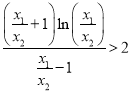 ,进而可知
,进而可知![]() .
.
解:(1)![]() ,若函数
,若函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 区间
区间![]() 上恒成立,所以
上恒成立,所以![]() .
.
令![]() ,则
,则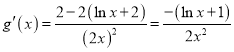 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,故
,故![]() ,所以实数a的取值范围a
,所以实数a的取值范围a![]() .
.
(2)由(1)可知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以,当![]() 时,
时,![]() ,则当
,则当![]() 时有
时有![]() ,
,
即![]() .因为当
.因为当![]() 时
时![]() ,所以
,所以![]() 时,
时,
![]() ,
,![]() ,
,
![]() ,……,
,……,![]() ,
,
所以![]()
![]() ,
,
即![]() ,所以
,所以![]() .
.
(3)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,不妨设
,不妨设![]() ,
,
即![]() 有两个相异实根
有两个相异实根![]() ,
,![]() ,且
,且![]() .
.
从而有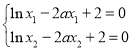 ,将上两式相加得:
,将上两式相加得:![]() .
.
将上两式相减得:![]() ,从而
,从而![]() ,
,
即![]() ,即得
,即得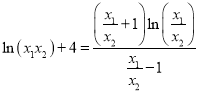 ,
,
要证明![]() ,也就是证明
,也就是证明![]() ,即
,即![]() ,
,
也就是证明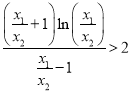 ,令
,令![]() ,只需证明
,只需证明![]() ,
,
由![]() ,知
,知![]() ,因此只需证明
,因此只需证明![]()
令![]() ,则
,则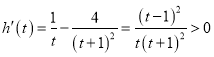 ,
,
所以![]() 在区间
在区间![]() 上单调递增,又因为
上单调递增,又因为![]() ,
,
因此![]() 在区间
在区间![]() 上恒成立.
上恒成立.
所以,当![]() 时,
时,![]() 成立,所以有
成立,所以有![]() 成立,从而
成立,从而![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为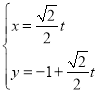 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
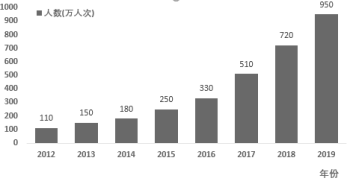
【题目】近年来,某市立足本地丰厚的文化旅游资源,以建设文化旅游强市,创建国家全域旅游示范市为引领,坚持以农为本,以乡为魂,以旅促农,多元化推动产业化发展,文化和旅游扶贪工作卓有成效,精准扶贫稳步推进.该市旅游局为了更好的了解每年乡村游人数的变化情况,绘制了如图所示的柱状图.则下列说法错误的是( )
0
A.乡村游人数逐年上升
B.相比于前一年,2015年乡村游人数增长率大于2014年乡村游人数增长率
C.近8年乡村游人数的平均数小于2016年乡村游人数
D.从2016年开始,乡村游人数明显增多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向体积为1的正方体密闭容器内注入体积为![]() 的液体,旋转容器,下列说法正确的是( )
的液体,旋转容器,下列说法正确的是( )
A.当![]() 时,容器被液面分割而成的两个几何体完全相同
时,容器被液面分割而成的两个几何体完全相同
B.![]() ,液面都可以成正三角形形状
,液面都可以成正三角形形状
C.当液面与正方体的某条体对角线垂直时,液面面积的最大值为![]()
D.当液面恰好经过正方体的某条体对角线时,液面边界周长的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年以来,世界经济和贸易增长放缓,中美经贸摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性.今年以来,商务部会同各省市全面贯彻落实稳外贸决策部署,出台了一系列政策举措,全力营造法治化、国际化、便利化的营商环境,不断提高贸易便利化水平,外贸稳规模、提质量、转动力取得阶段性成效,进出口保持稳中提质的发展势头,下图是某省近五年进出口情况统计图,下列描述正确的是( )
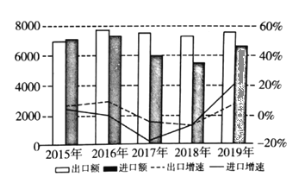
A.这五年,2015年出口额最少B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降D.这五年,2019年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本4元,且以9元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂.根据以往100天的资料统计,得到如表需求量表:
需求量/个 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
天数 | 15 | 25 | 30 | 20 | 10 |
该蛋糕店一天制作了这款蛋糕X(X∈N)个,以x(单位:个,100≤x≤150,x∈N)表示当天的市场需求量,T(单位:元)表示当天出售这款蛋糕获得的利润.
(1)当x=135时,若X=130时获得的利润为T1,X=140时获得的利润为T2,试比较T1和T2的大小;
(2)当X=130时,根据上表,从利润T不少于560元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润T关于市场需求量x的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为ξ,求随机变量ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
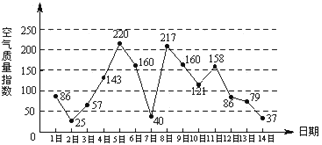
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com