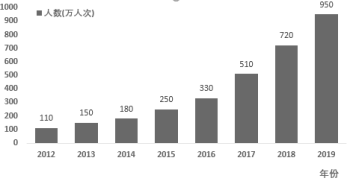
【题目】近年来，某市立足本地丰厚的文化旅游资源，以建设文化旅游强市，创建国家全域旅游示范市为引领，坚持以农为本，以乡为魂，以旅促农，多元化推动产业化发展，文化和旅游扶贪工作卓有成效，精准扶贫稳步推进.该市旅游局为了更好的了解每年乡村游人数的变化情况，绘制了如图所示的柱状图.则下列说法错误的是（ ）
0
A.乡村游人数逐年上升
B.相比于前一年，2015年乡村游人数增长率大于2014年乡村游人数增长率
C.近8年乡村游人数的平均数小于2016年乡村游人数
D.从2016年开始，乡村游人数明显增多
科目：高中数学 来源： 题型：
【题目】(13分)
在平面直角坐标系xOy中，抛物线
上异于坐标原点Ｏ的两不同动点Ａ、Ｂ满足
（如图所示）．
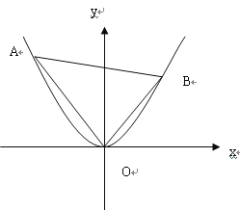
（Ⅰ）求
得重心Ｇ（即三角形三条中线的交点）的轨迹方程；
（Ⅱ）
的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】受疫情影响，某电器厂生产的空调滞销，经研究决定，在已有线下门店销售的基础上，成立线上营销团队，大力发展“网红”经济，当线下销售人数为
（人）时，每天线下销售空调可达
（百台），当线上销售人数为
（人）（
）时，每天线上销量达到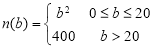
（百台）.
（1）解不等式：
，并解释其实际意义；
（2）若该工厂大有销售人员
（
）人，按市场需求，安排人员进行线上或线下销售，问该工厂每天销售空调总台数的最大值是多少百台？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的离心率为
，且与抛物线
交于
，
两点，
（
为坐标原点）的面积为
．
（1）求椭圆的方程；
（2）如图，点
为椭圆上一动点（非长轴端点）
，
为左、右焦点，
的延长线与椭圆交于
点，
的延长线与椭圆交于点，求
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知曲线
的参数方程为：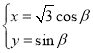
，（
为参数），以坐标原点为极点，
轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为
（1）求曲线和直线l的直角坐标方程；
（2）若点
在曲线上，且点到直线l的距离最小，求点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
（1）若函数
在区间
上单调递减，求实数a的取值范围；
（2）当
，（
）时，求证：
；
（3）若函数有两个极值点
，
，求证：
（e为自然对数的底数）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中， 
，动点
满足：以
为直径的圆与
轴相切.
（1）求点
的轨迹方程；
（2）设点
的轨迹为曲线
，直线
过点
且与
交于
两点，当
与
的面积之和取得最小值时，求直线
的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的左、右焦点为
，
，点
在椭圆上，且
面积的最大值为
，周长为6.
（1）求椭圆的方程，并求椭圆的离心率；
（2）已知直线
：
与椭圆交于不同的两点
，若在
轴上存在点
，使得
与中点的连线与直线垂直，求实数
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
