练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，已知曲线的参数方程为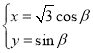：，（为参数），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为

    （1）求曲线和直线l的直角坐标方程；

    （2）若点在曲线上，且点到直线l的距离最小，求点的坐标.

    【答案】（1）：，：；（2）

    【解析】

    （1）由曲线的参数方程化为，平方相加，求得曲线的直角坐标方程，把直线的极坐标方程化为，进而求得直线的直角坐标方程；

    （2）设点，求得点到直线的距离，结合三角函数的性质，即可求解.

    （1）由曲线的参数方程为：，（为参数），可得，

    平方相加，可得，即曲线的直角坐标方程为，

    由直线的极坐标方程化为，

    将，代入可得，

    故直线的直角坐标方程为.

    （2）由点在曲线上，设点，

    则点到直线的距离

    当时，即，点到直线的距离的最小值为，

    此时点的坐标为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若圆锥的内切球（球面与圆锥的侧面以及底面都相切）的半径为1，当该圆锥体积取最小值时，该圆锥体积与其内切球体积比为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆M：，直线l：（）过定点N，点P是圆M上的任意一点，线段的垂直平分线和相交于点Q，当点P在圆M上运动时，点Q的轨迹为曲线C.

    （1）求曲线C的方程；

    （2）直线l交C于A，B两点，D，B关于x轴对称，直线与x轴交于点E，且点D为线段的中点，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，等腰梯形ABCD中，AB∥CD，AD＝AB＝BC＝1，CD＝2，E为CD中点，以AE为折痕把△ADE折起，使点D到达点P的位置（P平面ABCE）．

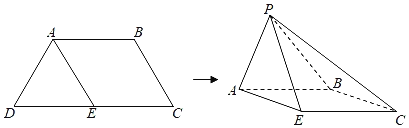
    （1）证明：AE⊥PB；

    （2）若直线PB与平面ABCE所成的角为，求二面角A﹣PE﹣C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

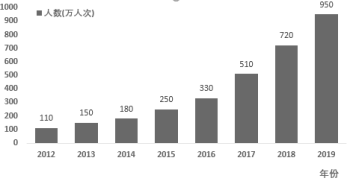
    【题目】近年来，某市立足本地丰厚的文化旅游资源，以建设文化旅游强市，创建国家全域旅游示范市为引领，坚持以农为本，以乡为魂，以旅促农，多元化推动产业化发展，文化和旅游扶贪工作卓有成效，精准扶贫稳步推进.该市旅游局为了更好的了解每年乡村游人数的变化情况，绘制了如图所示的柱状图.则下列说法错误的是（ ）


    0

    A.乡村游人数逐年上升

    B.相比于前一年，2015年乡村游人数增长率大于2014年乡村游人数增长率

    C.近8年乡村游人数的平均数小于2016年乡村游人数

    D.从2016年开始，乡村游人数明显增多

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱柱中，已知底面为等腰梯形，，，M，N分别是棱，的中点

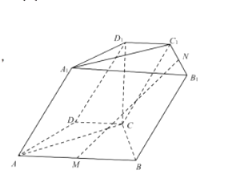
    （1）证明：直线平面；

    （2）若平面，且，求经过点A，M，N的平面与平面所成二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求曲线在点处的切线方程；

    （2）若函数有两个极值点，，且不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于，若数列满足，则称这个数列为“K数列”．

    （Ⅰ）已知数列：1，m+1，m2是“K数列”，求实数的取值范围；

    （Ⅱ）是否存在首项为-1的等差数列为“K数列”，且其前n项和满足

    ？若存在，求出的通项公式；若不存在，请说明理由；

    （Ⅲ）已知各项均为正整数的等比数列是“K数列”，数列不是“K数列”，若，试判断数列是否为“K数列”，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求的单调区间；

    （2）若在处取得极值，直线与的图象有三个不同的交点，求的取值范围.若的极大值为1，求的值.

    查看答案和解析>>

    同步练习册答案