
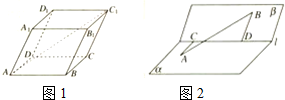
 下列说法正确的个数为( )
下列说法正确的个数为( ) | A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 举例说明①错误;由共面向量基本定理说明②正确;分别利用空间向量求解AC1与α,β所成二面角说明③④错误.
解答 解:①由向量共线定理可知,当$\overrightarrow{b}=\overrightarrow{0}$时不成立,故①错误;
②由2$\overrightarrow{OP}=x\overrightarrow{OA}-y\overrightarrow{OB}+z\overrightarrow{OC}$,得$\overrightarrow{OP}=\frac{x}{2}\overrightarrow{OA}-\frac{y}{2}\overrightarrow{OB}+\frac{z}{2}\overrightarrow{OC}$,
∵x-y+z=2,∴$\frac{x}{2}-\frac{y}{2}+\frac{z}{2}=1$,则P与A,B,C共面,故②正确;
③∵${\overrightarrow{A{C}_{1}}}^{2}=(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{C{C}_{1}})^{2}$=${\overrightarrow{AB}}^{2}+{\overrightarrow{BC}}^{2}+{\overrightarrow{C{C}_{1}}}^{2}$+2$\overrightarrow{AB}•\overrightarrow{BC}+2\overrightarrow{BC}•\overrightarrow{C{C}_{1}}+2\overrightarrow{AB}•\overrightarrow{C{C}_{1}}$
=1+1+1+2×1×1×cos60°+2×1×1×cos60°+2×1×1×cos60°
=6.∴|AC1|=$\sqrt{6}$,故③错误;
④设二面角α-l-β的平面角为θ,AC⊥l,BD⊥l,
AC=BD=CD=1,AB=2,∴${\overrightarrow{AB}}^{2}=(\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB})^{2}={\overrightarrow{AC}}^{2}+{\overrightarrow{CD}}^{2}$$+{\overrightarrow{DB}}^{2}+$$2|\overrightarrow{AC}||\overrightarrow{DB}|cosθ$,
∴4=1+1+1-2cosθ,解得cosθ=-$\frac{1}{2}$,∴α,β所成二面角为120°,故④错误.
∴正确命题的个数是1个.
故选:D.
点评 本题考查命题的真假判断与应用,考查了空间向量在求解问题中的应用,是中档题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,边长为2的正方形ABCD中,点E在AB边上,点F在BC边上,
如图,边长为2的正方形ABCD中,点E在AB边上,点F在BC边上,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2) | B. | [$\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+3i | B. | -1+2i | C. | $\sqrt{10}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图为一个几何体的三视图,其中俯视图为正三角形,左视图是长为2,宽为4的矩形,
如图为一个几何体的三视图,其中俯视图为正三角形,左视图是长为2,宽为4的矩形,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com