
分析 (1)去绝对值,分x<-1,-1≤x≤1,x>1讨论,再解一次不等式,求并集即可;
(2)求得二次函数的最小值,以及分段函数的最大值,由恒有公共点,可得m的不等式,解得m的范围.
解答 解:(1)当m=5 时,f(x)=5-|x-1|-|x+1|
=$\left\{\begin{array}{l}{5+2x,x<-1}\\{3,-1≤x≤1}\\{5-2x,x>1}\end{array}\right.$,…3分
由f(x)>2得不等式的解集为{x|-$\frac{3}{2}$<x<$\frac{3}{2}$}.…5分
(2)由二次函数y=x2+2x+3=(x+1)2+2,
该函数在x=-1 取得最小值2,
因为f(x)=$\left\{\begin{array}{l}{m+2x,x<-1}\\{m-2,-1≤x≤1}\\{m-2x,x>1}\end{array}\right.$,在x=-1 处取得最大值m-2,…8分
所以要使二次函数y=x2+2x+3与函数y=f(x)的图象恒有公共点,
只需m-2≥2,即m≥4.…10分
点评 本题考查分段函数的运用:解不等式,注意运用分类讨论,考查恒成立思想的运用,考查运算能力,属于中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | 4 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,7] | B. | [0,7] | C. | [-2,7] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
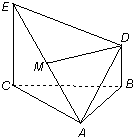 如图△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD=a,M是EA的中点.(1)求证:(1)DM∥平面ABC;
如图△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD=a,M是EA的中点.(1)求证:(1)DM∥平面ABC;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
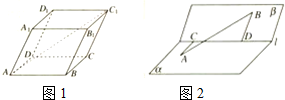 下列说法正确的个数为( )
下列说法正确的个数为( ) | A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-2) | C. | [-6,+∞) | D. | [-6,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com