
 如图,边长为2的正方形ABCD中,点E在AB边上,点F在BC边上,
如图,边长为2的正方形ABCD中,点E在AB边上,点F在BC边上,分析 (Ⅰ)由题设条件知:A'D⊥A'E,A'D⊥A'F,A'E∩A'F=A',由此能够证明A'D⊥面A'EF,从而得到A'D⊥EF;
(Ⅱ)由题意求得A′F=A′E=$\frac{3}{2}$,EF=$\frac{\sqrt{2}}{2}$,进一步求出△A′EF的面积,又A′D是三棱锥D-A′EF的高线,可以算出三棱锥D-A′EF的体积,即为三棱锥A′-DEF的体积.
解答 (Ⅰ)证明:∵边长为2的正方形ABCD中,E、F是AB、BC的中点,将△AED、△DCF分别沿DE、DF折起,使AC两点重合于点A′,
∴A'D⊥A'E,A'D⊥A'F,A'E∩A'F=A',
∴A'D⊥面A'EF,
∵EF?面A'EF,∴A'D⊥EF;
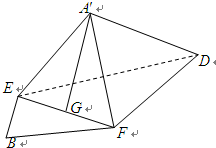
(Ⅱ)解:∵BE=BF=$\frac{1}{4}$BC=$\frac{1}{2}$,∴A′F=A′E=$\frac{3}{2}$,EF=$\frac{\sqrt{2}}{2}$,
在△A′EF中,可得A′G=$\sqrt{(\frac{3}{2})^{2}-(\frac{\sqrt{2}}{4})^{2}}=\frac{\sqrt{34}}{4}$,
∴△A′EF的面积为${S}_{△A′EF}=\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{34}}{4}=\frac{\sqrt{17}}{8}$,
∵A′D⊥平面A′EF.
∴A′D是三棱锥D-A′EF的底面A′EF上的高线,
因此,三棱锥A′-DEF的体积为:${V}_{A′-DEF}=\frac{1}{3}•{S}_{△A′EF}•A′D$=$\frac{1}{3}×\frac{\sqrt{17}}{8}×2=\frac{\sqrt{17}}{12}$.
点评 本题考查异面直线垂直的证明,考查三棱锥的体积的求法,注意翻折变换中数量关系的变化,合理地进行等价转化,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2k-1,2k+2](k∈Z) | B. | [2k+1,2k+3](k∈Z) | C. | [4k+1,4k+3](k∈Z) | D. | [4k+2,4k+4](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | 4 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{16},0)$ | B. | $(\frac{π}{9},0)$ | C. | $(\frac{π}{4},0)$ | D. | $(\frac{π}{2},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
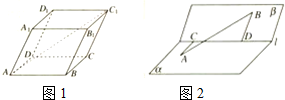 下列说法正确的个数为( )
下列说法正确的个数为( ) | A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com