
分析 根据题意,结合函数的奇偶性与单调性分析可得:若f(x)=f(1-$\frac{1}{x+3}$)=f($\frac{x+2}{x+3}$),则|x|=|$\frac{x+2}{x+3}$|,结合一元二次方程根与系数的关系可得每个方程的两根之积,将其相乘即可得答案.
解答 解:根据题意,函数f(x)是定义在R上的偶函数,且在(0,+∞)是单调函数,
则f(x)在(-∞,0)上也单调,
若f(x)=f(1-$\frac{1}{x+3}$)=f($\frac{x+2}{x+3}$)
则必有|x|=|$\frac{x+2}{x+3}$|,即±x=$\frac{x+2}{x+3}$,
若x=$\frac{x+2}{x+3}$,即x2+2x-2=0,则x1•x2=-2,
若-x=$\frac{x+2}{x+3}$,即x2+4x+2=0,则x3•x4=2,
∴故方程|x|=|$\frac{x+2}{x+3}$|有4个解,且4个解之积x1•x2•x3•x4=-4,
故选:-4.
点评 本题考查函数奇偶性与单调性的综合应用,注意函数在(0,+∞)上单调的含义,属于中档题


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:选择题
| A. | y=2x | B. | $y=\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tan(α+β)=3tan(α-β) | B. | tan(α+β)=2tan(α-β) | C. | 3tan(α+β)=tan(α-β) | D. | 3tan(α+β)=2tan(α-β) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
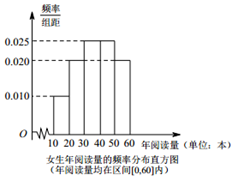 每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频数分布表和女生年阅读量的频率分布直方图.
每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频数分布表和女生年阅读量的频率分布直方图.| 本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 频数 | 3 | 1 | 8 | 4 | 2 | 2 |
| 性别 阅读量 | 丰富 | 不丰富 | 合计 |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 |
| k0 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com