
分析 (1)①根据等差数列和等差数列的前n项和公式,以及等差数列的性质,即可求出,
②若an+1≤bn<an+2,得到$\left\{\begin{array}{l}{{n}^{2}-n-\frac{2a}{d}≤0}\\{{n}^{2}+n-\frac{2a}{d}>0}\end{array}\right.$,解得即可,
(2)由已知条件可得$\frac{{q}^{t+1}-1}{t(t+2)}$=$\frac{{q}^{r+1}-1}{r(r+2)}$,构造f(n)=$\frac{{q}^{n+1}-1}{n(n+2)}$,n≥2,n∈N*,利用定义证明其单调性,再分别赋值验证即可.
解答 解:(1)①∵3b1,2b2,b3成等差数列,
∴4b2=3b1+b3,
即4×$\frac{3a+3d}{2}$=2(2a+d)+$\frac{4a+6d}{3}$,
∴d=$\frac{4}{3}$a,
∴$\frac{a}{d}$=$\frac{3}{4}$,
②由an+1≤bn<an+2,
得a+nd=$\frac{1}{n}$[(n+1)a+$\frac{1}{2}$n(n+1)d]<a+(n+1)d,
整理得$\left\{\begin{array}{l}{{n}^{2}-n-\frac{2a}{d}≤0}\\{{n}^{2}+n-\frac{2a}{d}>0}\end{array}\right.$,
解得$\frac{-1+\sqrt{1+\frac{8a}{d}}}{2}$<n≤$\frac{1+\sqrt{1+\frac{8a}{d}}}{2}$,
由于$\frac{1+\sqrt{1+\frac{8a}{d}}}{2}$-$\frac{-1+\sqrt{1+\frac{8a}{d}}}{2}$=1且得$\frac{-1+\sqrt{1+\frac{8a}{d}}}{2}$>0,
因此存在唯一的正整数n,使得an+1≤bn<an+2.
(2)∵$\frac{{b}_{t}}{{b}_{r}}$=$\frac{\frac{{a}_{1}(1-{q}^{t+1})}{t(1-q)}}{\frac{{a}_{1}(1-{q}^{r+1})}{r(1-q)}}$=$\frac{t+2}{r+2}$,
∴$\frac{{q}^{t+1}-1}{t(t+2)}$=$\frac{{q}^{r+1}-1}{r(r+2)}$,
设f(n)=$\frac{{q}^{n+1}-1}{n(n+2)}$,n≥2,n∈N*,
则f(n+1)-f(n)=$\frac{{q}^{n+2}-1}{(n+1)(n+2)}$-$\frac{{q}^{n+1}-1}{n(n+2)}$=$\frac{{q}^{n+1}[(q-1){n}^{2}+2(q-2)n-3]+2n+3}{(n+1)(n+3)n(n+2)}$,
∵q>2,n≥2,
∴(q-1)n2+2(q-2)n-3>n2-3≥1>0,
∴f(n+1)-f(n)>0,
即f(n+1)>f(n),
∴f(n)为单调递增,
∴当r≥2时,t>r≥2,
则f(t)>f(r),即$\frac{{q}^{t+1}-1}{t(t+2)}$>$\frac{{q}^{r+1}-1}{r(r+2)}$,这与$\frac{{q}^{t+1}-1}{t(t+2)}$=$\frac{{q}^{r+1}-1}{r(r+2)}$互相矛盾,
∴r=1时,即$\frac{{q}^{t+1}-1}{t(t+2)}$=$\frac{{q}^{2}-1}{3}$,
若t≥3,则f(t)≥f(3)=$\frac{{q}^{4}-1}{15}$=$\frac{{q}^{2}-1}{3}$•$\frac{{q}^{2}+1}{5}$>$\frac{{q}^{2}-1}{3}$,即$\frac{{q}^{t+1}-1}{t(t+2)}$>$\frac{{q}^{2}-1}{3}$,这与$\frac{{q}^{t+1}-1}{t(t+2)}$=$\frac{{q}^{2}-1}{3}$互相矛盾,
于是t=2,
∴$\frac{{q}^{3}-1}{8}$=$\frac{{q}^{2}-1}{3}$,
即3q2-5q-5=0,
∵q>2,
∴q=$\frac{5+\sqrt{85}}{6}$
点评 此题主要考查等差的性质的应用,题目较为复杂,需要一步一步的分析求解,计算量要求较高,属于难题.


科目:高中数学 来源: 题型:解答题
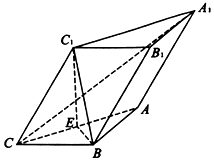 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{5}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{1}{3}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{2}{5}$,$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com