
| A. | ($\frac{1}{5}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{1}{3}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{2}{5}$,$\frac{\sqrt{2}}{2}$) |
分析 点Q(c,$\frac{a}{2}$)在椭圆的内部,$\frac{{b}^{2}}{a}>\frac{a}{2}$,|PF1|+|PQ|=2a-|PF2|+|PQ|,由-|QF2|+|PQ|≤|PQ|-|PF2|≤|QF2|,且|QF2|=$\frac{a}{2}$,要|PF1|+|PQ|<5|F1F2|恒成立,即2a-|PF2|+|PQ|≤2a+$\frac{a}{2}$<5×2c.
解答 解:∵点Q(c,$\frac{a}{2}$)在椭圆的内部,∴$\frac{{b}^{2}}{a}>\frac{a}{2}$,⇒2b2>a2⇒a2>2c2.
$\frac{c}{a}<\frac{\sqrt{2}}{2}$
|PF1|+|PQ|=2a-|PF2|+|PQ|
又因为-|QF2|+|PQ|≤|PQ|-|PF2|≤|QF2|,且|QF2|=$\frac{a}{2}$,
要|PF1|+|PQ|<5|F1F2|恒成立,即2a-|PF2|+|PQ|≤2a+$\frac{a}{2}$<5×2c
$\frac{5a}{2}<10c$,$\frac{c}{a}>\frac{1}{4}$,则椭圆离心率的取值范围是($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$).
故选:B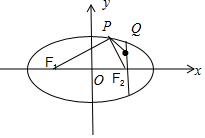
点评 本题考查了椭圆的方程、性质,椭圆的离心率,转化思想是解题关键,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{14}{3}$ | C. | 3或$\frac{14}{3}$ | D. | 3或$-\frac{11}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x | B. | $y=\frac{1}{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,8) | B. | (2,16) | C. | (4,8) | D. | $(2\sqrt{2},16)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | tan(α+β)=3tan(α-β) | B. | tan(α+β)=2tan(α-β) | C. | 3tan(α+β)=tan(α-β) | D. | 3tan(α+β)=2tan(α-β) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com