
分析 由题意作图辅助,从而可判断四边形为直角梯形,从而求其面积.
解答 解:由题意作图如右图,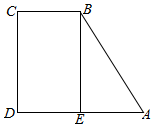
∵$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{AD}$,
∴BC∥AD且|BC|=$\frac{1}{2}$|AD|,
又∵|AB|=|AD|,且∠BAD=60°,
∴|AE|=$\frac{1}{2}$|AB|=$\frac{1}{2}$|AD|,
∴|BC|=|DE|,
∴BCDE是平行四边形,
∴CD∥BE,
∴DC⊥AD,
∵|CD|=$\sqrt{3}$,
∴|AB|=|AD|=2,
∴S=$\frac{1+2}{2}$$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$,
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题考查了学生的作图能力及数形结合的思想应用,属于中档题.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |z1|<|z2| | B. | |z1|=|z2| | C. | |z1|>|z2| | D. | 无法比较 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
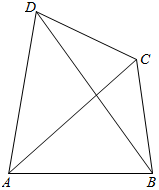 如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求
如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| A. | 210 | B. | 210.5 | C. | 211.5 | D. | 212.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com