
分析 (1)由题意的离心率公式,求得a=$\sqrt{2}$b,由椭圆过点(0,1),求得a和b的值,求得椭圆方程;
(2)将直线方程代入椭圆方程,由韦达定理,及向量数量积的坐标运算,求得B点坐标,求得直线BF2的斜率,即可求得直线BF2的方程.
解答 解:(1)由椭圆的斜率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{2}}{2}$,则a=$\sqrt{2}$b,
由点(0,1)则b=1,a=$\sqrt{2}$,
椭圆E的方程$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)设直线AB的直线方程y=k(x+1),A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:(1+2k2)x2+4k2x+2k2-2=0,
由韦达定理可知:x1+x2=-$\frac{4{k}^{2}}{1+2{k}^{2}}$,①,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$,②
$\overrightarrow{B{F}_{1}}$=2$\overrightarrow{{F}_{1}A}$,则(-1-x2,-y2)=2(x1+1,y1),则2x1+x2=-3,③
由①②可知:x1=$\frac{-2{k}^{2}-3}{1+2{k}^{2}}$,x2=$\frac{3-2{k}^{2}}{1+2{k}^{2}}$,
代入②整理得:2k2=7,解得:k=±$\frac{\sqrt{14}}{2}$,
则B(-$\frac{1}{2}$,±$\frac{\sqrt{14}}{4}$),
则直线BF2的斜率k=±$\frac{\sqrt{14}}{6}$,
∴直线BF2的方程:y=±$\frac{\sqrt{14}}{6}$(x-1).
点评 本题考查椭圆的标准方程及椭圆的离心率,考查直线与椭圆的位置关系,韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{3}$ | B. | 6π | C. | $\frac{17π}{3}$ | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | 2a>2b | C. | lga>lgb | D. | sina>sinb |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
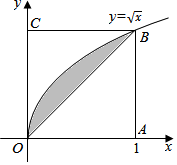 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好取自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)=$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{\sqrt{2}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [0,$\frac{\sqrt{6}}{3}$] | D. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0) | B. | (1,2] | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com